This lecture will talk about “Divide-and-Conquer”, which is a very powerful algorithm design technique. The main paradigm of it is shown in the following:

• Divede: If we are given some big problem and don’t know how to solve it in an efficient way, we can try to solve it into some small sub-problems.

• Conquer: Then we can conquer each problem recursively.

• Combine: Sometings, we need combine the solutions of these subproblems into the solution of the big problem.

Powering a number

Given a number ${ x \in \mathbb{R}}$, and a integer ${ n \geq 0 }$. Computer ${ x^n }$.

We can use “Divide-and-Conquer” strategy to solve this problem. For ${ x^n }$, we can treat it as ${ x^{n/2} \cdot x^{n/2} }$. So, we just need to solve the ${ x^{n/2} }$, and do one more time of multiplying to get ${ x^n }$. That’s the big picture of our idea. Let’s show it in detail.

Therefore, we can get the recurence of ${ T(n)}$

By Master Theorem, ${ T(n) = T(\lfloor n/2 \rfloor) + \Theta(1) = \lg n }$

Fibonacci numbers

The definiation of Fibonacci numbers

Naive recursive alg.

We can just calculate ${ F_n }$ by recursion. Drawing the recursion tree, we will find that the size of problem only decrease ${ 1 }$ or ${ 2 }$ in each step. Therefore, we can get the running time of this algorithm is ${ T(n) = \Omega(2^{n/2}) }$ and ${ T(n) = O(2^n) }$.

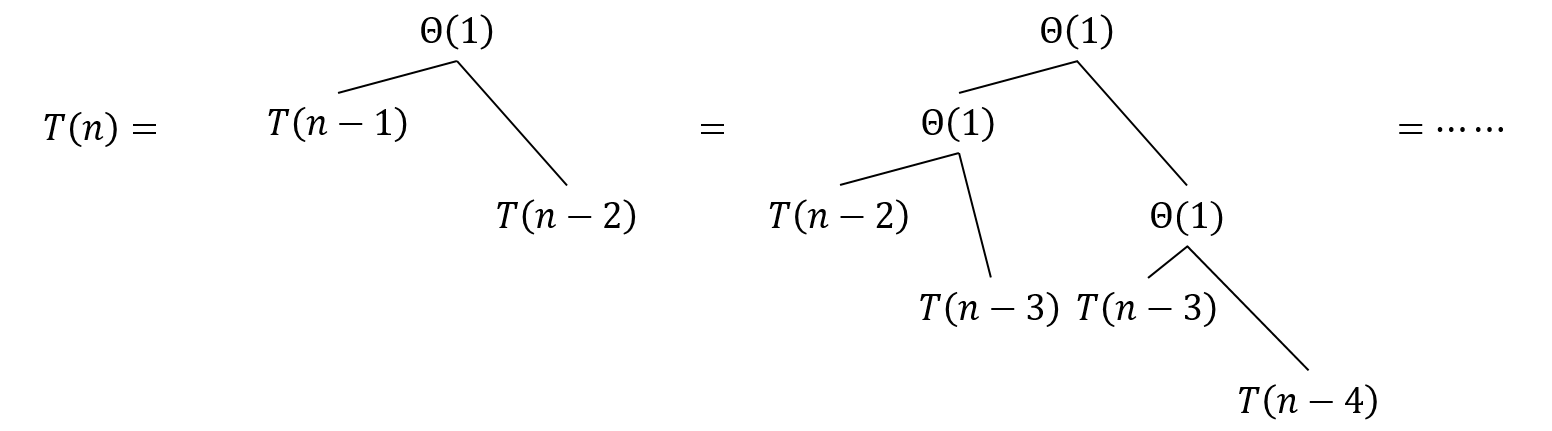
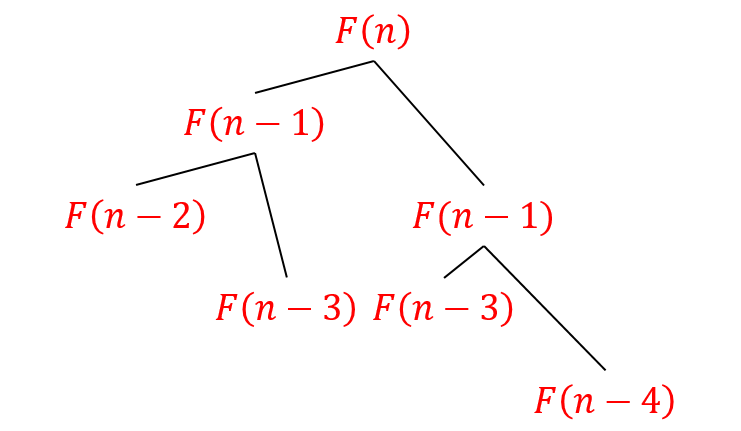
But we want a polynomial algorithm, so let’s move forward.

Bottom-up algorithm

Because in the above algorithm, we calculate a lot of repeat item in the tree. That’s not necessary! We can just calculate it from ${ F_1 }$!

1
2
3
4
5
6
7
8
9
10
11
12
13
Bottom_up_Fibonacci(n):
    if n == 1 or n == 2
        return 1
    else
        a = 1
        b = 1
        i = 0
        while i < n-2
            c = b
            b = a + b
            a = c
            i++
        return b

It’s easy to check the total running time is ${ T(n) = \Theta(n) }$

${ \require{cancel} \bcancel{\text{Naive recursive squaring} } }$

From the following General Term Formula, we can get ${ F_n = [\varphi^n / \sqrt{5}] ,\varphi = \frac{1+\sqrt{5}}{2}}$. We denote operation ${ [\cdot] }$ as taking the nearest integer.

Ideally, we can use the algorithm in last section to calculate ${ F_n = \varphi^n / \sqrt{5}}$ and take the nearest integer in ${ \Theta(\lg n) }$ time.

However the above operation cannot be finished in a real machine. That’s because our computer have to reperent numbers, like ${ \varphi, \sqrt{5}}$, as floating point numbers. That means, we have fixed amount of precise bits, which can not promise we get the correct answer when we take nearest integer!!

Recursive squaring (${ \checkmark }$)

Therefore, we can computer ${ F_n }$ by nth power of that 2-by-2 matrix. And, the multiplication of two 2-by-2 matrices only need a constant running time. Therefore, we can compute ${ \left( \matrix{1&1\\1&0} \right)^n }$ in ${ \Theta(\lg n) }$ time by the strategy mentioned in Section #1.

General Term Formula

For Fibonacci Sequence, we want to find its General term formula. We want find an appropriate cofficient ${ \lambda }$ to make ${A_n = F_n - \lambda F_{n-1} }$ become a geometrical sequence

We can solve the equation ${ \frac{1}{-\lambda} =\frac{1-\lambda}{1}}$ to get ${ \lambda = \frac{1\pm \sqrt {5}}{2} }$. We can select ${ \lambda = \frac{1- \sqrt {5}}{2} }$, then the ratio ${ q }$ of ${ A_n }$ is ${ \frac{1+ \sqrt {5}}{2} }$, that means

So, we can get ${ A_n = q^{n-2}A_2}$. Hence, we can solve ${ F_n }$ by ${ F_n -\frac{1- \sqrt {5}}{2} \cdot F_{n-1}= q^{n-2}A_2 }$, that is (note ${ \lambda \cdot q = -1 }$)

Matrix multiplication

Let’s recap the definition of Matrix multiplication. Suppose we have matrix ${ A\in\mathbb{R}^{n\times n}=[a_{ij}], B\in\mathbb{R}^{n\times n}=[b_{ij}]}$, So ${ C= A\cdot B\in\mathbb{R}^{n\times n}=[c_{ij}] }$

Standard Algorithm

We can write down an algorithm directly by definition, and the psedocode is shown in the following

1
2
3
4
5
6
7
8
Matrix_Multiplication(A,B):
    n = size_of(A)
    let C be a new n*n matrix
    for i = 1 to n
        for j = 1 to n
            c_ij = 0
            for k = 1 to n
                c_ij = c_ij + a_ik * b _kj

It’s easy to check the above algorithm take ${ \Theta (n^3)}$ running time.

Divide-and-conquer alg.

If we consider “Divide-and-conquer” strategy, we will have the following idea:

For a ${ n\times n }$ matrix, we can treat is a ${ 2\times 2 }$ block matrix of ${ n/2 \times n/2 }$ submatrix (here we suppose ${ n = 2^k, k\in \mathbb{N}^+ }$). We can show it as follow

And, we can check

That means, to calculate ${ C }$, we need to recursively do the following operation

Notice the above operation, we will find that we need do ${ 8 }$ recursive multiplication of ${ n/2 \times n/2 }$ matrix, and ${ 4 }$ addtion of ${ n/2 \times n/2 }$ matrix. So we can get the recurrence of cost (we add two items in the same postion of two matrix together, which need be done for ${ n^2/4 }$ times)

By Master theorem, we solve the recurrence ${ T(n) = \Theta (n^{\log_2 8}) = \Theta (n^3) }$. It’s a suck result, we don’t improve our running time. BUT! The recurrence can give us some inspiration.

Strassen Algorithm

The whole idea of Strassen Algorithm is making the cofficient ahead of the ${ T(n/2) }$ become smaller, that means we need to decrease the times of multiplication. To complete it, we don’t care about the extra addition opertaion, because it only costs ${ \Theta(n^2) }$ time.

Then, we can use the above matrices ${ P_1,\cdots ,P_7 }$ to calculate ${ C_{11},C_{12},C_{21},C_{22} }$

Notice that the above operations only take ${ 7 }$ multiplication. So, the recurrence is ${ T(n) = 7 T(n/2) + \Theta(n^2)= \Theta(n^{\log_2 7})=O(n^{2.81}) }$

PS: how about ${ n }$ is odd

Actually, we will meet the situation that ${ n }$ is odd, so we hit some bumps during using Strassen Algorithm. But, don’t worry! We can pad the matrices with zeros to solve it!

We will use the following fact

Here the two padded matrices are ${ N\times N }$. In other words, we pad ${ N-n }$ columns and ${ N-n }$ rows of zeros into original matrices.

In practice, we can pad the matrices recursively. When ${ n }$ is odd, we can pad it into ${ (n+1) \times (n+1) }$ matrix, and call Strassen Algorithm to compute the multiplication.

VLSI layout Problem.

VLSI (Very Large_Scale Integration) problem is embed a completed binary tree with ${ n }$ leaves into a grid with minimum area.

naive embedding

We can first come up a naive idea like the following figure. Therefore, we can write down the recurrence of the height ${ h(n) }$ and width ${ w(n) }$. ${ h(n) = h(n/2) + \Theta(1)=\Theta(\lg n), w(n) = 2w(n/2) + O(1) =\Theta(n) }$. Therefore the area is ${ n \lg n }$.

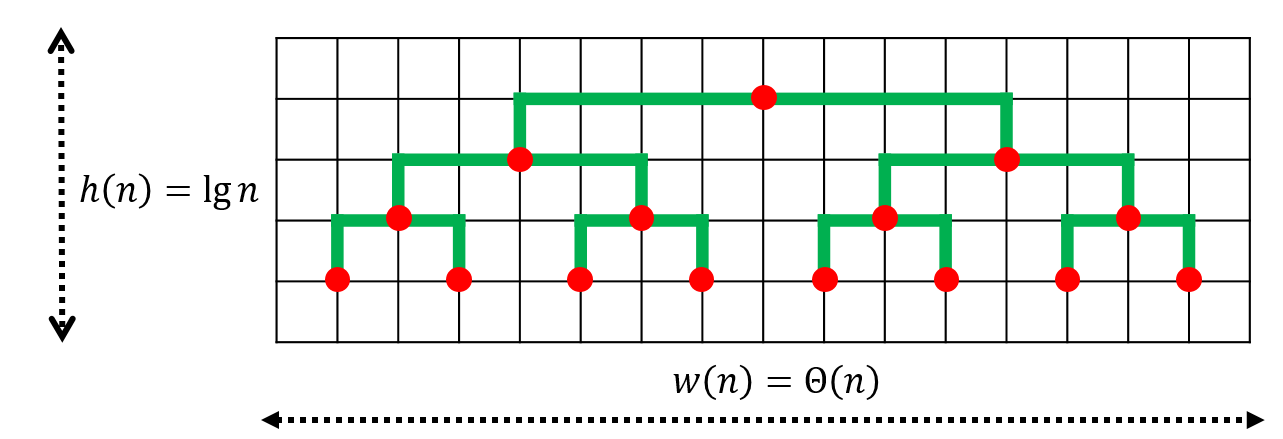
Can we do better? Maybe we can try ${ \Theta(\sqrt {n}) \cdot \Theta(\sqrt {n}) }$!!

So, what kind of recurrence is ${ \Theta(\sqrt {n})}$? We can guess ${ T(n) = 2T(n/4) + O(n^{1/2-\varepsilon}) }$.

H layout

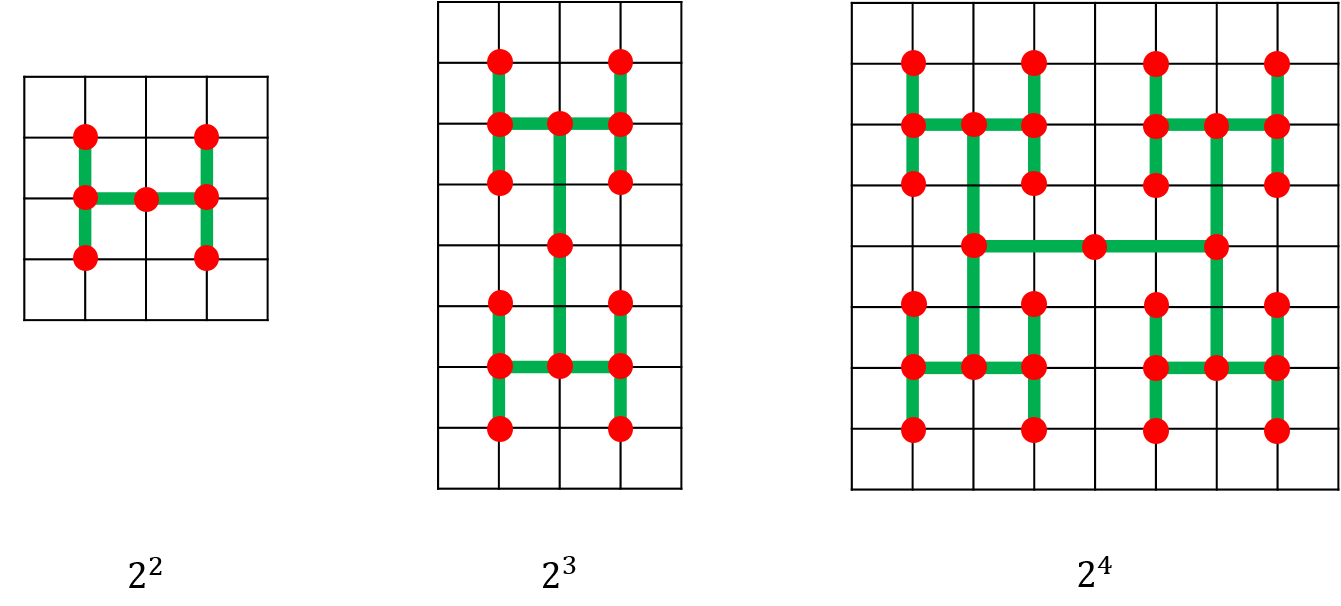
Why we take “H”, because we want divide ${ n }$ into ${ 4 }$ part! And each part will have ${ n/4 }$ leaves! The root note is the middle！It’s easy to check ${ h(n) = 2h(n/4) + \Theta(1)= \Theta(\sqrt {n}), w(n) = 2w(n/4) + \Theta(1) = \Theta(\sqrt {n})}$.

So, we get the area that is ${ \Theta(n) }$