Thsi blog is still talking about hardness of problems, focusing on NP, NP-Complete Problems.
Definition of NP
Problems and Algorithms
The input to a computational problem will be encoded as a finite binary string ${ s }$. We denote the length of a string ${ s }$ by ${ \vert s \vert }$.
We will identify a decision problem X with the set of strings on which the answer is “yes.” An algorithm ${ A }$ for a decision problem receives an input string ${ s }$ and returns the value “yes” or “no” — we will denote this returned value by ${ A(s) }$. We say that ${ A }$ solves the problem ${ X }$ if for all strings ${ s }$, we have ${ A(s) = yes }$ if and only if ${ s \in X }$.
we say that ${ A }$ has a polynomial running time if there is a polynomial function ${ p(\cdot) }$ so that for every input string ${ s }$, the algorithm ${ A }$ terminates on ${ s }$ in at most ${ O(p(\vert s \vert)) }$ steps.
Efficient Certification
A “checking algorithm” for a problem ${ X }$ has a different structure, we need input string ${ s }$ and a separate “certificate” string ${ t }$ that contains the evidence that ${ s }$ is a “yes” instance of ${ X }$.
Thus we say that ${ C }$ is an efficient certifier for a problem ${ X }$ if
-
${ C }$ is a polynimial-time algorithm that takes two input arguments ${ s }$ and ${ t }$.
-
We have ${ s \in X }$ if and only if there exists a string ${ t }$ such that ${ \vert t \vert \leq poly(\vert s \vert) }$ and ${ C(s,t) = yes }$
It’s toooooo abstract definition! Let’s give an example to try to understand it.
For Independent Set Problem ${ X }$ (here ${ X }$ is the set of all the yes instances in decision IS problem). We may hard to know instance ${ (G,k)\in X }$ is “yes” or “no”), but here we use the Certification way to do it. Let’s give a concerate vertex set ${ S \in G }$ with at least ${ k }$ vertices, actully this set ${ S }$ is a “certificate” string ${ t }$. And the algorithm ${ C }$ is to check whether this set ${ S }$ is a independent set (check whether there have edges in ${ S }$). So, ${ C(s,t)= yes, s = (G,k) }$ iff ${ s \in X }$. That’s clear, if ${ S }$ is indeed a independent set of ${ G }$ with at least ${ k }$ vertices, it’s no doubt ${ s=(G,k) }$ is a yes instance.
Definition of NP
-
P Problem: decision problems with polytime algortihm.
-
NP Problem: decision problems with polytime certifier (efficient certifier).
-
EXP Problem: decision problems with exponential time algorithm.
Claim 1 ${ P \subseteq NP }$
Proof. Consider a problem ${ X \in P }$, that means there exists a polynomial algorithm ${ A}$, that can solving the problem ${ X }$. That is ${ \forall s \in X }$, ${ A(s) = yes }$. Hence, for the certifier, we can set ${ t = \emptyset }$, and ${ C(t,s) = A(s) }$, it’s easy to check ${ C(t,s) =yes }$ iff ${ A(s) =yes }$. So ${ X \in NP }$, that means ${ P \subseteq NP }$. ${ \square }$
Claim 2 ${ NP \subseteq EXP }$
Proof. ${\forall X \subseteq NP }$, By definition, ${ \forall s \in X }$, ${ \exists }$ a polytime certifier ${ C(s,t) }$ with the size of ${ t }$ is poly ${ poly(\vert s \vert }$. To solve ${ s }$, we can run ${ C(s,t) }$ for all possible certificate ${ t }$. So there exists ${ exp(\vert x\vert) }$ choices for ${ t }$. And we can return yes if there exists ${ t }$ such that ${ C(s,t) }$. Otherwise, ${ s }$ is a no instance. Hence, ${ X \in EXP }$. ${ \square }$.
Defnition of NP-Complete
Definition of NP-Complete A problem ${ X}$ is NPC if
- ${ X \in NP }$
- ${ \forall Y \in NP }$, ${ Y\leq_p X }$
Claim 3 Let ${ X }$ be an NPC problem, then ${ X \in P }$ iff ${ P = NP }$.
Proof. If ${ P = NP }$, ${ X \in P }$
If ${ X \in P }$, and ${ \forall Y \in NP, Y \leq_p X}$, so ${ Y \in P }$. Hence, ${ NP \subseteq P }$, that means ${ NP = P }$ because ${ P \subseteq NP }$. ${ \square }$
Strategy to prove NPC
Let ${ X }$ be an already-known NPC Problem. Now to show ${ Y }$ is NPC
-
${ Y \in NP }$
-
${ X \leq_p Y }$.
By transitivity we can prove any NP problem can reduce to ${ Y }$. Now, we need to prove first NPC problem!!
First NPC problem – CKT-SAT
Definition of Circuit Satisfiability
Circuit Satisfiability (CKT-SAT): Given a circuit ${ K }$, directed acyclic graph (directed tree) with boolean gates ${ \land, \lor,\lnot }$ as nodes as below
-
The sources (the bottom leaves with no incoming edges) in ${ K }$ are labeled either with one of the constants ${ 0 }$ or ${ 1 }$, or with the name of distinct variable. The nodes with variables will become the inputs to ${ K }$.
-
Every other node is labeled with one of the Boolean operators. Nodes with ${ \land, \lor }$ have two incomming edge and nodes with ${ \lnot }$ have one incoming edge.
-
The root node (the only one node with no outgoing edges) will represent the output.
So the Circuit Satisfiability (CKT-SAT) problem is, given a circuit ${ K }$, does there exists any input assignment so that output is ${ 1 }$.
CKT-SAT is NPC
Proof.
- Show ${CKT-SAT \in NPC}$.
The certificate ${ t }$ can be the assignment of each inputs. And the certifier ${ C(K,t), K\in CKT-SAT }$ is the algorithm to compute the output of circuit ${ K }$, which is polynomial. So ${CKT-SAT \in NPC}$.
- Show ${ \forall X \in NP }$, ${ X \leq_p CKT-SAT}$.
As ${ X \in NP }$, it has a polynomial certifier ${ C(x,t), x \in X }$ such that ${ t \leq poly(\vert x \vert) }$. Hence, if we want to solve ${ X }$, we equivalently transfer it to another problem: “is there exists a ${ t }$ such that ${ t \leq poly(\vert x \vert) }$ so that ${ C(x,t) = yes }$?”
We will transfer this problem to CKT-SAT, that means if we can solve CKT-SAT, we can solve ${ X }$. Following is the construction. Because, certifier ${ C }$ indeed exists, we can transfer it to a computer, which consists of real circuits. We can take instance ${ x }$ as constants (given value) in leaves and certificate ${ t }$ as variables (input). It’s clear this CKT-SAT problem have an assignment that output ${ 1 }$ iff ${ C(x,t) =yes }$. ${ \square }$
Using Stratgy
Prove 3-SAT is NPC
Proof.
-
3-SAT ${ \in NP }$. We can take a satisfiable assignment ${ t }$ as certifier, and the algorithm check whether input is satisfiable is a polynomial certifier.
-
CKT-SAT ${ \leq_p }$ 3-SAT
For any instance ${ K\in }$ CKT-SAT, we will construct a 3-SAT instance by it as follow.
(a) For each edge in the circuit ${ K }$, creat a SAT variable ${ x_i }$.
(b) For each node ${ v }$ labeled with ${ \lnot }$, suppose the incoming edge is ${ u }$, we need to guarantee ${ x_v = \overline{x_u} }$. We can use two clauses ${ (x_v \lor x_u) }$ and ${ (\overline{x_v} \lor \overline{x_u}) }$ to replace.
Showing the equivalence.
${\Rightarrow}$: if ${ x_v = \overline{x_u} }$, it's easy to check ${ (x_v \lor x_u) = 1}$ and ${ (\overline{x_v} \lor \overline{x_u}) =1}$; ${\Leftarrow}$: if ${ (x_v \lor x_u) =1}$ and ${ (\overline{x_v} \lor \overline{x_u}) = 1 }$, assume ${ x_v \neq \overline{x_u} }$, that means ${ x_v = x_u }$, so we cannot guarantee ${ (x_v \lor x_u) }$ and ${ (\overline{x_v} \lor \overline{x_u}) }$ is ${ 1 }$ at the same time.(c) For each node ${ v }$ labeled with ${ \lor }$, and its two incoming edges are ${ u }$ and ${ w }$. We need to have ${ x_v = x_u \lor x_w }$. We can use three clauses ${ (x_v \lor \overline{x_u}) }$, ${ (x_v \lor \overline{x_w}) }$ and ${ (\overline{x_v} \lor x_u \lor x_w) }$ to replace.
Showing the equivalence.
If ${ x_v = 1 }$, we need either ${ x_u = 1 }$ or ${ x_w =1 }$. It's trivial ${ (x_v \lor \overline{x_u}) = 1 }$ and ${ (x_v \lor \overline{x_w}) = 1 }$. And ${ x_u = 1 }$ or ${ x_w =1 }$ is equivalent to ${ (\overline{x_v} \lor x_u \lor x_w) = (0 \lor x_u \lor x_w) = 1}$. If ${ x_v = 0 }$, we need both ${ x_u = 0 }$ and ${ x_w = 1 }$. It's trivial ${ (\overline{x_v} \lor x_u \lor x_w) = 1 }$. And ${ x_u = 0 }$ and ${ x_w = 1 }$ is equivalent to ${ (x_v \lor \overline{x_u}) =1 }$, ${ (x_v \lor \overline{x_w}) = 1}$(d) For each node ${ v }$ labeled with ${ \land }$, and its two incoming edges are ${ u }$ and ${ w }$. We need to have ${ x_v = x_u \land x_w }$. We can use three clauses ${ (\overline{x_v} \lor x_u) }$, ${ (x_v \lor \overline{x_w}) }$ and ${ (x_v \lor \overline{x_u} \lor \overline{x_w}) }$ to replace.
Showing the equivalence.
Similar with above discussion. Consider ${ x_v = 0 }$ or ${ 1 }$.(e) For each constant leaf ${ v }$, we set clause ${ x_v }$ if the constant is ${ 1 }$. Otherwise ${ \overline{x_v} }$. (Easy to check)
(f) The output node ${ o }$ set clause ${ x_o }$.
(g) Now, we fill each clause to three literals. For each clause with two literals, ${ (x_v \lor x_w) }$, we replace it as two clauses ${ (x_v \lor x_w \lor x_w) \land (x_v \lor x_w \lor \overline{x_w}) }$. For one literal ${ x_v }$, replaced as ${ (x_v \lor x_w) \land (x_v \lor \overline{x_w}) }$.
If we have a assignment to 3-SAT instance, it’s easy to get the variables of leaves is an assignment to CKT-SAT instance. And, if we already have a assignment to inputs of CKT-SAT, we can use all literals described before as an assignment to 3-SAT problems.
${ 3 }$-SAT ${ \leq_p }$ ${ 3 }$ coloring
Graph Coloring Porblem: Given a graph ${ G }$, we want to color each node such that no two adjacent nodes get the same color.
${ k }$ Coloring Porblem: Given a graph ${ G }$ and a parameter ${ k }$, can ${ G }$ be colored with ${ k }$ colors?
${ 2- }$coloring problem
${G }$ has a valid ${ 2 }$-coloring iff ${ G }$ is a bipartite graph. We can use BFS or DFS to check a graph if is a bipartite graph.
Prove ${ 3 }$ coloring is NPC
Proof.
- ${ 3 }$ coloring ${ \in NP }$.
We can pick up a valid 3-coloring assignment to each nodes as a certificate ${ t }$. And the algortithm check each edge ${ \{u,v\} }$ if has a conflict nodes coloring, that is ${ color{u) \neq color(v} }$.
- ${ 3 }$ coloring ${ \leq_p }$ ${ 3 }$-SAT
Given an instance ${ \phi \in 3-SAT }$, with ${ n }$ variables and ${ m }$ clauses ${ c_1, c_2,\cdots,c_m }$.
We will creat a graph ${ G }$ as following
-
Creat a triangle with three nodes ${ T, F, B }$. (Spoiler: We will use three colors named ${ T,F, B }$, and we are going to assign “True” to variables with ${ T }$ color and “False” to variables with ${ F }$ color.)
-
For each variable ${ x_i \in \phi}$, we add two nodes ${ v_i }$ and ${ \overline{v_i} }$. And we connected ${ v_i }$, ${ \overline{v_i} }$ and ${ B }$ to each other.
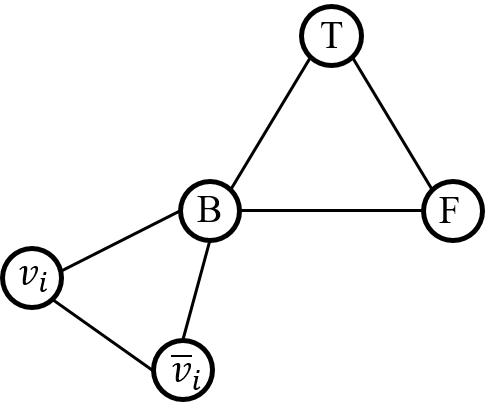
- Observation 1 We will find, in this structure, the nodes representing literals can only be labeled as ${ T }$ or ${ F }$, and ${ v_i, \overline{v_i} }$ will be assigned to different labels. (Because they are connected to each other)
- For each clauses, we will use following “OR” gadget to represent it. Following figure show the structure representing clause ${ (a\lor \overline{b} \lor c) }$ (For readability, in the left side we draw the “B” node in triangle repeatedly).
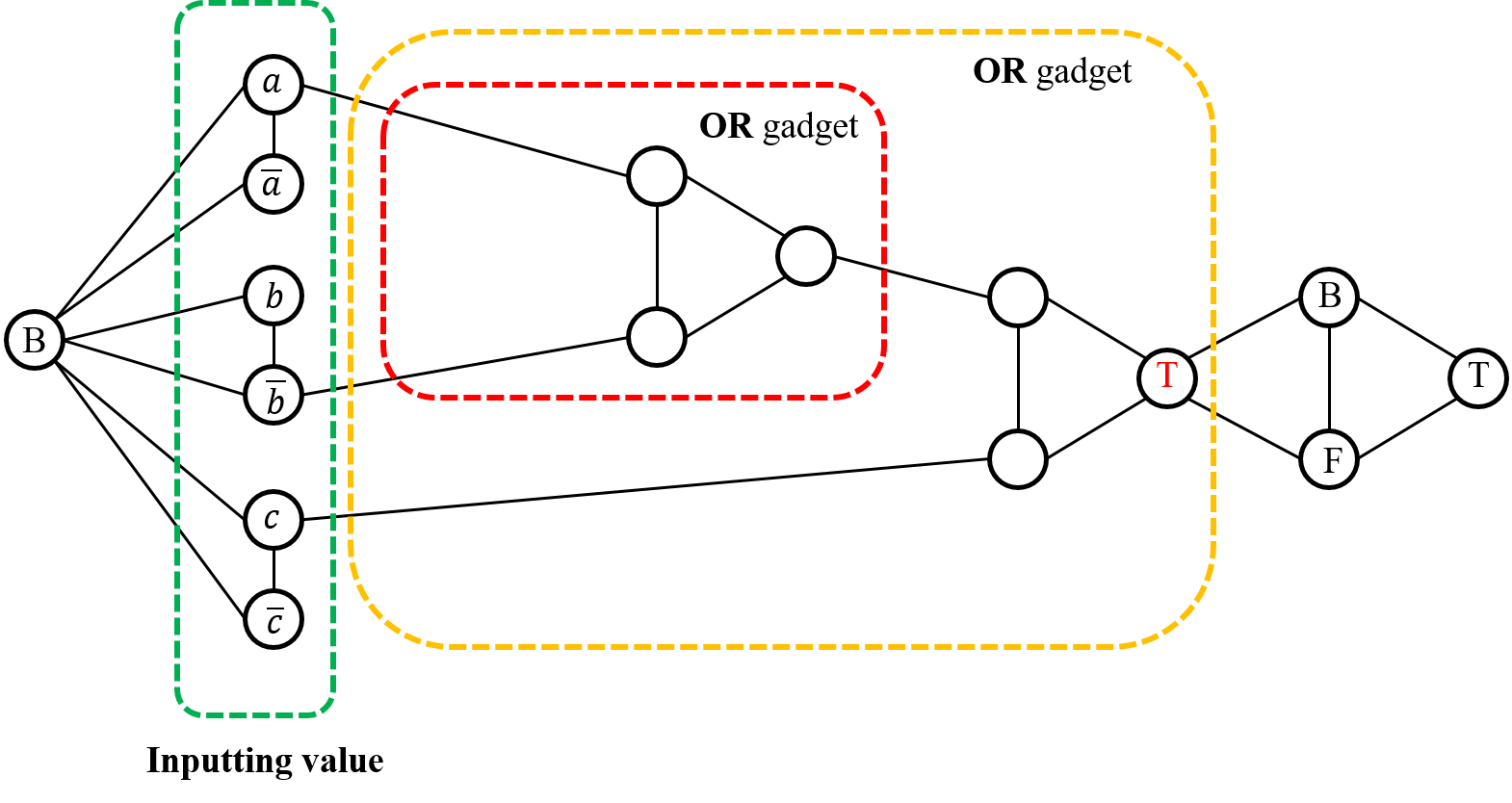
-
Observation 2 The output node in OR gadget must be ${ T }$, due to it link to ${ B }$ and ${ F }$.
-
Observation 3 We will find the structure in the red box is a “OR” structure. If one of the literals is True, we can given a valid coloring plan to each nodes. If all the literals are False, the last nodes must be ${ F }$ which is conflict to Observation 2.
Following we will show the equivalence.
${\Rightarrow}$: If we have a True assignment to 3-SAT instance ${ \phi }$, we can first, assign ${ T }$ or ${ F }$ to the nodes in graph as their boolean value. And, then because it’s a true assignment, we can always find a suitable coloring plan to fill the nodes in gadget. Hence, we have a 3-coloring plan in ${ G }$.
${\Leftarrow}$: If we have a valid 3-coloring plan ${ T,B,F }$ in ${ G }$ and we set the initial triangle with our designing color, we can get the boolean value from the variable nodes by the color ${ T }$ or ${ F }$. Because, ${ G }$ indeed have a 3-coloring plan. So, each clause represented by a gadget is True. Otherwise, we cannot find a valid 3-coloring in the gadget.