This blog talks about the Ford-Fulkerson Algorithm to solve the max flow problem.

Greedy Alogrithm (idea)

For following flow problem

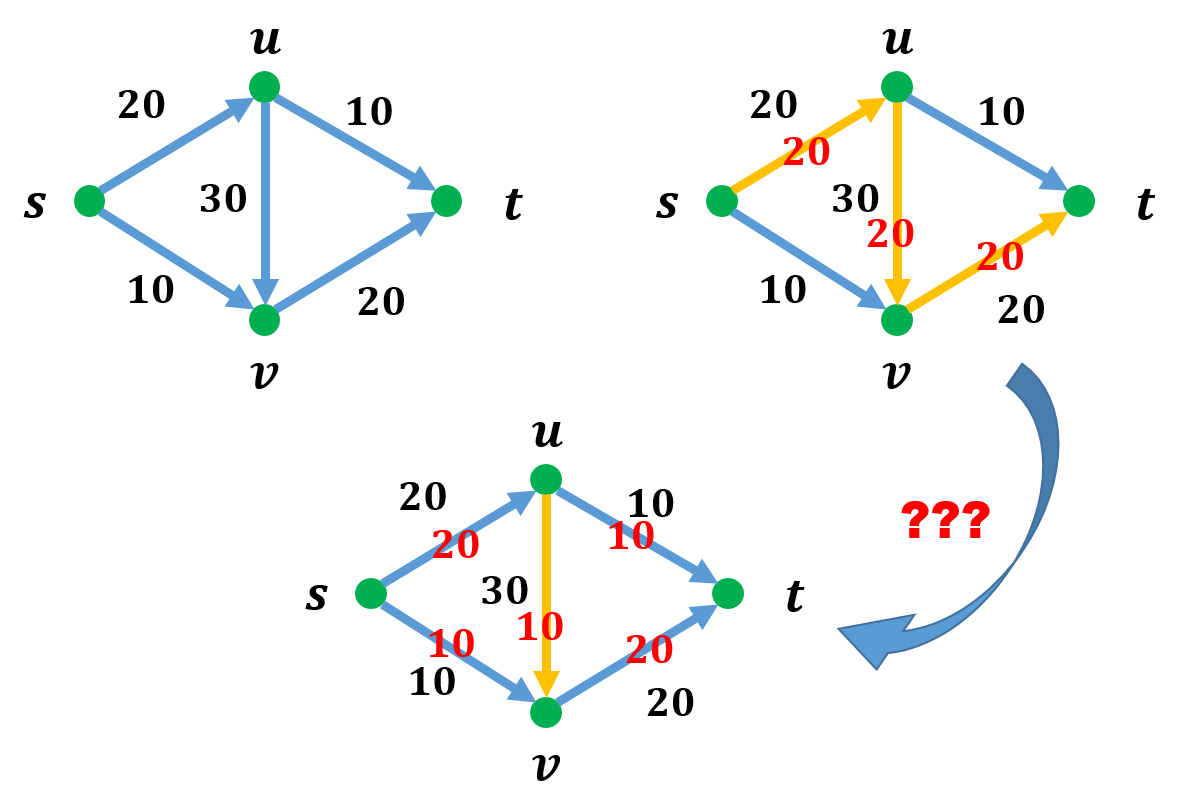
If we pick up a path and add flow to them, like ${ s \rightarrow u \rightarrow v \rightarrow t }$. We can assign a flow with ${ 20 }$ in this path. And, we will find, we can not find another path to add flow. But, the below one is the max flow. So, what should I do to change the right one to below one?

We need a chance to modify our anwser. We hope to withdraw the flow on edge ${ (u,v) }$. This observation leads to the idea of “Residual Graph” and Ford-Fulkerson algorithm.

Ford-Fulkerson Algorithm

Residual Graph

Given a graph ${ G }$ and a flow ${ f }$, we can define the “Residual Graph” ${ G_f = (V_f,E_f)}$.

We keep all the nodes from ${ G }$ in ${ G_f }$. But for each edge in ${ G }$, we will define a backward edge for original edge (forward edge). We define the edge ${ E_f }$ as follow

And we assign capacity to each edge in ${ G_f }$ as below

Augmenting Path

We define a path as Augmenting Path if this path exists in residual graph ${ G_f }$.

We can easy to have the following observation.

Observation: If there exists an augmenting path in residue graph ${ G_f }$, then the current flow is not yet a max flow.

We will use this observation to design Ford-Fulkerson Algorithm. And we will prove it later.

Pseudocode

The basic idea of algorithm is

1. Finding a path ${ P }$ in the residual graph.

2. Finding the bottleneck capacity ${ b }$ of ${ P }$.

3. Augment flow of value ${ b }$ along ${ P }$.

4. Construct the new residual graph and continue until the current residual graph has no ${ s-t }$ path.

Here I will give the pseudocode as below

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Ford-Fulkerson(G,s,t,C)
    for each e in E
        f(e) = 0
    G_f = Residual(G,f)
    while (there exists augmenting path P in G_f)
        f = Augment_Flow(f,c,P)
        G_f = Residual(G,f)
    return f

Augment_Flow(f,c,P)
    b = bottleneck capacity of P
    for each e in P
        if e in E
            f(e) = f(e) + b
        else // e is backeard edge
            f(e) = f(e) - b
    return f

Residual(G,f)
    E_f = E
    for each e in E
        if 0 < f(e) < c(e)
            c(e) = c(e) - f(e)
            E_f = E_f + {e}
            c(e) = f(e)
        else if f(e) = c(e)
            E_f = E_f - {e} + {e_R}
            c(e_R) = f(e)
    G_f = G(V,E_f,C)
    return G_f

Correctness

Lemma 1 flow is valid

Proof. If we want show the flow is valid, we will show 1) the flow meets the capacity constraint and 2) the flow is conservative.

We can prove it by induction. Denote the current flow is $f$, and generate flow $f’$ after augment. We augment value $b$ in each iteration, which is a bottleneck value among augmenting path. For the forward edge $e$ in this augment path, $b \leq c(e) - f(e)$, hence $f’(e)= f(e) +b\leq c(e)$. For the backward edge $e’$, we know the value of its forward edge $e$ deduct $b$, that is $f’(e) = f(e) - b$. Due to $b \leq f(e)$, we have $0 \leq f’(e) = f(e) - b \leq c(e)$.

For the conservation constraints, we will also show in by induction.

• Base case: $f \equiv 0$, which means the flow is conservative.
• Induction Hypothesis, before $i$th iteration, flow is conservative, denote it as $f$.
• We will show after $i$th augmenting, we get $f’$, which is also a conservative flow. We consider the nodes in the augmenting path $P$ except $s,t$
  • Case 1: $e^F \rightarrow v \rightarrow e^F$. For node $v\in P$, it has a forward edge $e_1$ toward $v$ and has a forward edge $e_2$ leaving $v$. So, the flow in $e_1, e_2$ will both increase $b$. So the flow in node $v$ is still conservative.
  • Case 2: $e^F \rightarrow v \rightarrow e^B$. For node $v\in P$, it has a forward edge $e_1$ toward $v$ and has a backward edge $e’_2$ leaving $v$, which implies the forward edge $e_1$ increase value $b$ and the forward $e_2$ toward $v$ decrease $b$, so $v$ is still conservative.
  • Case 3: $e^B \rightarrow v \rightarrow e^F$. Similarly.
  • Case 3: $e^B \rightarrow v \rightarrow e^B$. Similarly.

By induction, the flow resulting by algorithm is conservative and meets the capacity constraint. $\square$

Output flow is maximum

We will show following three statements are equivalent which implies the augmenting path algorithm will output the maximum flow. And this proof also implies the Max Flow-Min Cut Theorem.

(1) $\exists$ a cut $(S,T)$ such that for some flow $f$ in $G$, $v(f) = cap (S,T)$.

(2) Flow $f$ is a max flow.

(3) There doesn’t exist any augmenting path in $G_f$.

Proof.

(1) $\Rightarrow$ (2): We can prove it by the lemma 2 and lemma 3 mentioned in last blog, which also implies the cut $(S,T)$ is a min cut.

(2) $\Rightarrow$ (3): Suppose there still have an augmenting path $P$ in $G_f$. We can push a flow by a positive value which contradicts to $f$ is a max flow.

(3) $\Rightarrow$ (1): This proof is more complex than above two, we need to construct a $s-t$ cut $S,T$ by current flow $f$ which lead to that There doesn’t exist any augmenting path in $G_f$. We construct $S,T$ as below:

$S$: Let $S$ be the set of vertices reachable from source $s$ in $G_f$.

$T$: $T := V \setminus S$. (Because, there doesn’t have any augmenting path, $t$ is not reachable from $s$, we have $t \in T$)

It’s clear $(S,T)$ is a valid $s-t$ cut in $G$.

Claim 1: For each edge $e=(u,v)$ in $G$ such that $u\in S, v \in T$, we have $f(e) = c(e)$.

Otherwise, $f(e) < c(e)$ then there exists an edge in $G_f$, and $u$ is reachable from $s$, now $v$ is also reachable, which contradicts to the construction rule of $S$. Q.E.D.

Claim 2: For each edge $e=(u,v)$ such that $u \in T , v \in S$, we have $f(e)= 0$.

Otherwise, its reverse edge $e^B=(v,u)$ is an edge in $G_f$, which means $u$ is reachable from $s$, which contradicts to the construction rule of $S$. Q.E.D.

By above two claim, we have

Hence, we find a $s-t$ cut $(S,T)$ that has same value to a flow $f$. $\square$

Running time

Assumption:

1. All capacities are integers and each capacity equals and less than ${ C }$.

2. Every flow value ${ f(e) }$ are integers.

The algorithm needs at most ${ mC }$ iterations. And each iteration takes time ${ O(m+n) = O(m) }$. And the total time is ${ O(m^2 C) }$. It’s a pseudo-polynomial time algorithm.