MLP简介
下面我们正式开始介绍深度学习。首先介绍最基本的全连接神经网络,它的结构比较简单,由输入层,输出层,隐藏层构成。所谓的输入层就是我们原始的特征向量,比如你设计了一个100维度的特征向量,那么输入层就是100个节点。输出层就是你需要得到结果的维度,比如你是一个二分类问题,你可以输出层是1个节点,也可以设计为两个节点,分别表示属于某个类别的概率。而隐藏层则是为了增加网络的复杂程度,更好的拟合输入输出直接的关系。
层与层之间的结构如下示意图所示,前一层与后一层的节点之间,两两相连。那么,怎么运算呢?对于后一层的每个节点而言,前一层的每个节点乘以一个权重,再求和然后加上一个偏移量${ b }$。然后,我们设计一个激活函数${ \sigma }$,比如Sigmoid、ReLU、Tanh(双曲正切)等等。然后就得到了该节点的值,如果有多层的话,这个过程不断重复。其实我们可以发现,这个过程第一步其实是一个线性变换,第二步是一个非线性的变换。这样保证了,网络可以去拟合比较复杂的关系。所以,其实每一层的传播可以写成${ H^{(L+1)} = \sigma(H^{(L)}W + b) }$的形式。
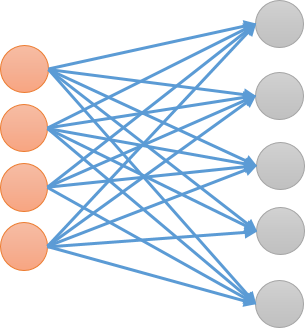
全连接层的应用场景还是比较广泛的,可以直接用于分类、回归等问题。也可以融合进别的模型之中,①将特征压缩映射到一个新的空间(即embeding),在这个空间也许更容易实现我们的任务;②将抽象的特征进行分类,起到分类器的的作用。换而言之,用在第一步,把特征嵌入到某个新空间中,或者用在最后一步,完成最终的分类或者回归任务。
过拟合
在机器学习算法里面,过拟合一直是一个常见的问题。它指的是,我们对于训练集的这些样本过于精确的吻合,但是用于预测新的数据效果非常差。这个问题大家应该很容易理解,理论上给定训练集,设计一个足够复杂、参数足够多的模型总是可以完美的拟合所有样本点,但是这个却不是不我们需要的,我们需要的是寻找到一个可靠的规律,能够去帮我们解决新的问题。举个例子就是,过拟合就是死学课本变成书呆子,不会举一反三,考试仍然考不好。
解决过拟合问题,有下面这几个常用的办法。
停止训练
这个是最简单的办法,我们通过验证集上的损失值进行观察,如果已经收敛就可以终止训练不再进行。
Dropout
我们可以设置Dropout率,每一层随机失活一定比例的神经元,通过这样的方法,简化网络,使得模型的泛化能力更强。
正则化
我们知道,无论何种网络模型,优化的目标就是使得损失函数最小。那么,为了防止模型过于复杂导致过拟合,我们可以通过给损失函数增加正则项的方法来约束模型参数。常用有${ l_1,l_2 }$范数。${ l_1 }$范数称为Lasso回归,目的是使得参数的绝对值之和最小化。 ${ l_2 }$范数成为岭回归,目的是为了参数的平方和最小化。
CNN简介
卷积层
CNN在传统上用来处理图像数据,对于图像数据而言,其本质就是一个矩阵,每个元素表示一个像素点,如果是黑白图片,那么值代表一个灰度。如果是RGB这样的彩色图片,我们往往将R、G、B视为三个通道(Channel),也就是有三个矩阵,每个像素点的RGB值分别储存在三个矩阵的对应位置。那么所谓的卷积操作,就是我们设计一个卷积核,比如下图1所示的是一个${ 3\times 3 }$的卷积核,也就是一个${ 3\times 3 }$的矩阵。我们用这个矩阵扫描整张图片,扫描到一个特定的位置(也是一个${ 3\times 3 }$的局部,那么卷积核和这个局部对应位置的值相乘并求和)

卷积操作.1
其实我个人认为,其实卷积操作也是一种特征提取,无非这个操作用在了二位矩阵上面。我们用卷积核提取一个更精炼的特征,用以下游的任务。
使用卷积的时候,会发现需要设置in_channels和out_channels两个参数,比如输入是RGB图片,也就是3个Channel,我们可以设置输出为${ C }$个channel,这是怎么实现的呢?其实也很简单,网络会产生${ C }$个不同的卷积核,但是size都是一致的,对于每个卷积核,将其在三个通道上扫描的结果相加,得到输出的一个通道,${ C }$个卷积核则会输出${ C }$个Channel.
如果我们不选择${ 1\times 1 }$的卷积核,那么卷积处理之后矩阵的size一定会改变。有时候我们希望卷积核处理过的矩阵保持原来的维度,那么我们往往会采用padding的操作,也就是在矩阵的四周补上适当的“0”,来保证卷积后的矩阵维度不变。如下图所示2
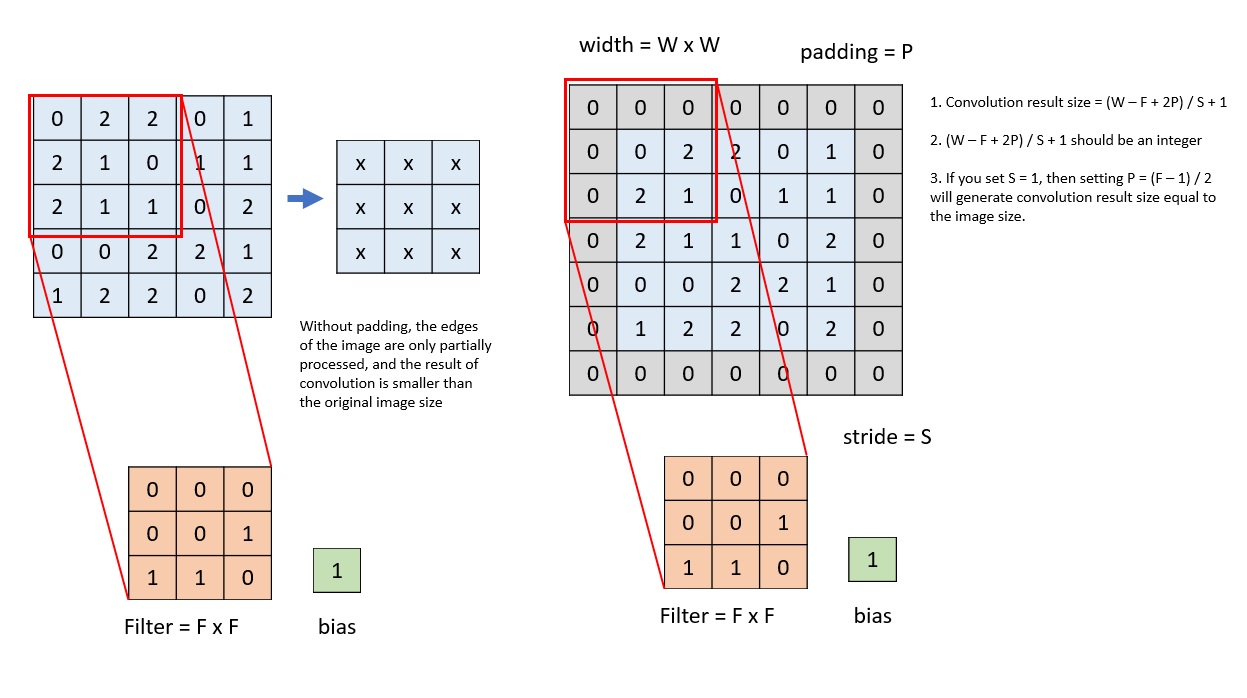
Padding操作.2
对于卷积的各种操作,描述起来往往有些复杂抽象,但是如果用图片或者动图来展示就会豁然开朗。这里放上一个很形象的各种类型卷积的动图展示链接。
池化层
池化操作往往接在卷积后面进行,主要目的是为了进一步提取特征,一般有两种最大池化和平均池化。顾名思义,我们选定池化核的尺寸以后,将整个待扫描的矩阵进行分区,每个区域计算最大值(或者平均值),也就是整个区域最后只得到一个值,所以维度降低。如下图所示3
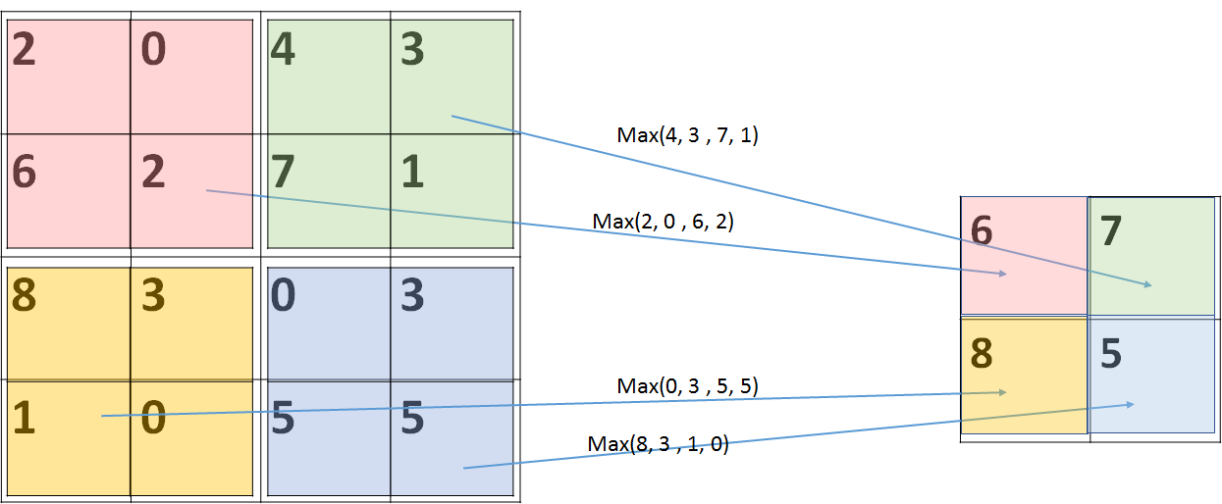
Pooling操作.3