GCN简介

下面的内容我想介绍一些比较潮流的网络模型。首先我们来介绍一下图卷积神经网络，严格来讲，我们想要完整的介绍图神经网络，应从图上卷积的定义开始讨论，然后介绍图上的傅里叶变换，以及基于谱域的图神经网络，最终不断简化成现在经典的图卷积网络。但是这里面的理论确实非常复杂，最起码对我而言，我看着略感头痛。那我们就抛弃理论，选择一个更符合直觉的思路来介绍，按照大部分图神经网络书上的写法，我们这种思路（理解方式）应该称为空域图神经网络。

我们从CNN开始谈起，其实对于图片而言，我们把像素视为界点，四周的像素与中心像素连边，我们也可以得到一个图，那么所谓的CNN其实就是将欧几里得距离比较近的点，它们的信息进行一个聚合。那么图卷积，就是一个很自然的扩展，我们把临近节点的信息进行整合。

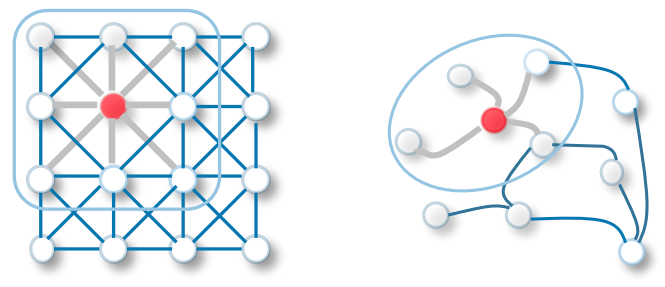
CNN vs GCN.¹

我们首先来看一下逐层传播的规则，也就是看看公式

$$ H^{(l+1)} = \sigma \left(\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} H^{(l)}W^(l)\right) $$

式子里面${ \tilde{A} = A + I_N }$，也就是邻接矩阵加上单位阵，说白了就是每个节点加上一个自环，其实也可以理解，否则更新权重的时候，就没有自身信息，全是邻居节点的信息了。${ \tilde{D} }$是一个度的矩阵，即${ \tilde{D} = \sum_j A_ij }$（对角线元素），其实进行的是一个归一化操作。${ H^{(l)} }$是上一层的节点特征矩阵。${ W^{(l)} }$是权重矩阵，待学习的参数。（矩阵的size为${ (N\times N) (N \times In) (In \times Out) = (N\times Out)}$）

这个公式猛一看不太好观察每个节点的特征发生了什么变化，那么对于节点${ v_i }$，逐层传播的公式为

$$ \begin{align} h^{(l+1)}_{v_i} &= \sigma \left(\sum_{j=1}^n c_{ij} h^{(l)}_{v_j}W^{(l)} \right) \\ & = \sigma \left(\sum_{v_j\in \mathcal{N}(v_i)\cup{v_i}}^n c_{ij} h^{(l)}_{v_j}W^{(l)}\right) \end{align} $$

这里面的${ c_ij }$为

$$ \begin{equation} c_{ij}= \left\{ \begin{aligned} &= \frac{1}{\sqrt{deg(v_i)deg(v_j)}} &\text{if } v_j \text{ is adjacent to } v_j,\\ &= 0&otherwise.\\ \end{aligned} \right. \end{equation} $$

所以，每个节点确实就是周围邻居节点乘以某个权重矩阵，再乘以归一化系数，最后相加的结果。这也就是下面这个经典的图片的含义。

GCN².

通过对于GCN的单层传播的介绍，我们可以发现，通过增加图卷积的层数，我们就可以整合${ k }$阶紧邻的信息，但是需要注意一个严重的问题，如果图卷积的层数太深，以及图是完全图，都需要注意，每个节点的信息会非常接近，会导致各种下游任务的失效，这就是所谓的过平滑。这里呢，我们只介绍了最初始的GCN模型，目前还衍生出各种各样的图神经网络。在此不一一介绍。

那么图神经网络可以做什么事情呢

1.节点分类，我们使用图神经网络，将节点特征嵌入一个新的空间后，可以用全连接神经网络来预测节点的标签。

2.链路预测，比如最简单的思路，在节点的特征嵌入新空间以后，用${ \sigma(z^T_i z_j) }$来预测${ v_i,v_j }$之间存在边的概率。（后文的VGAE就是这样的思路）

3.图分类，也就是我们给每个图一个标签，在GCN处理得到新的特征矩阵以后，用各种方式得到图的向量表示（均值、池化、加和等等），再用全链接网络预测图的标签。