We are going to talk about Piecewise linear convex objective functions. But before it, we will give some concepts, convex, concave and affine function.
Convex and concave function
Given two points ${ \bar{x}, \bar{y} \in \mathbb{R}^n}$
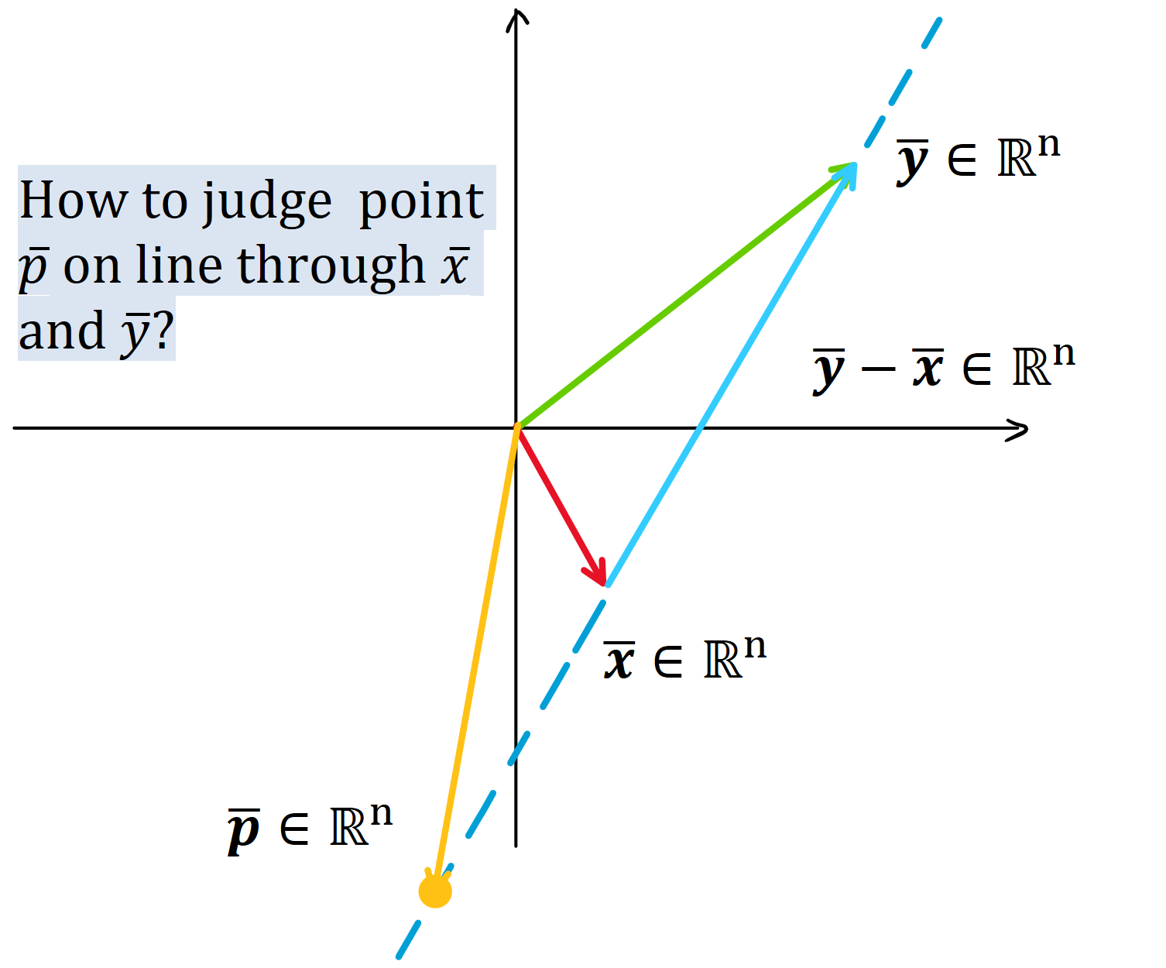
- A point ${ \bar{p} }$ is on the line through ${ \bar{x}, \bar{y} }$ iff ${ \exists \lambda \in \mathbb{R} }$ such that ${ \bar{p} - \bar{x} = \lambda(\bar{y}- \bar{x}) }$ i.e.
${ \Rightarrow }$ Here ${ \bar{p} }$ is a linear combination of ${ \bar{x}, \bar{y} }$ and the sum of their coefficients equals to ${ 1 }$.
${ \Rightarrow }$ Thus the line through ${ \bar{x}, \bar{y} }$ is the set ${ \{ (1-\lambda) \bar{x} + \lambda \bar{y} \vert \lambda \in \mathbb{R} \}}$.
- A point ${ \bar{p} }$ is on the segment of line joining ${ \bar{x} }$ to ${\bar{y} }$ iff ${ \bar{p} = (1-\lambda) \bar{x} + \lambda \bar{y}, 0\leq \lambda \leq 1 }$
${ \Rightarrow }$ Thus the segment of line joining ${ \bar{x} }$ to ${\bar{y} }$ is the set ${ \{ (1-\lambda) \bar{x} + \lambda \bar{y} \vert \lambda \in [0,1] \}}$.
Definition: A function ${ f: \mathbb{R}^n \rightarrow \mathbb{R} }$ is called convex if for every pair of points ${ \bar{x}, \bar{y} \in \mathbb{R}^n }$ and every ${ \lambda \in [0,1] }$, we have
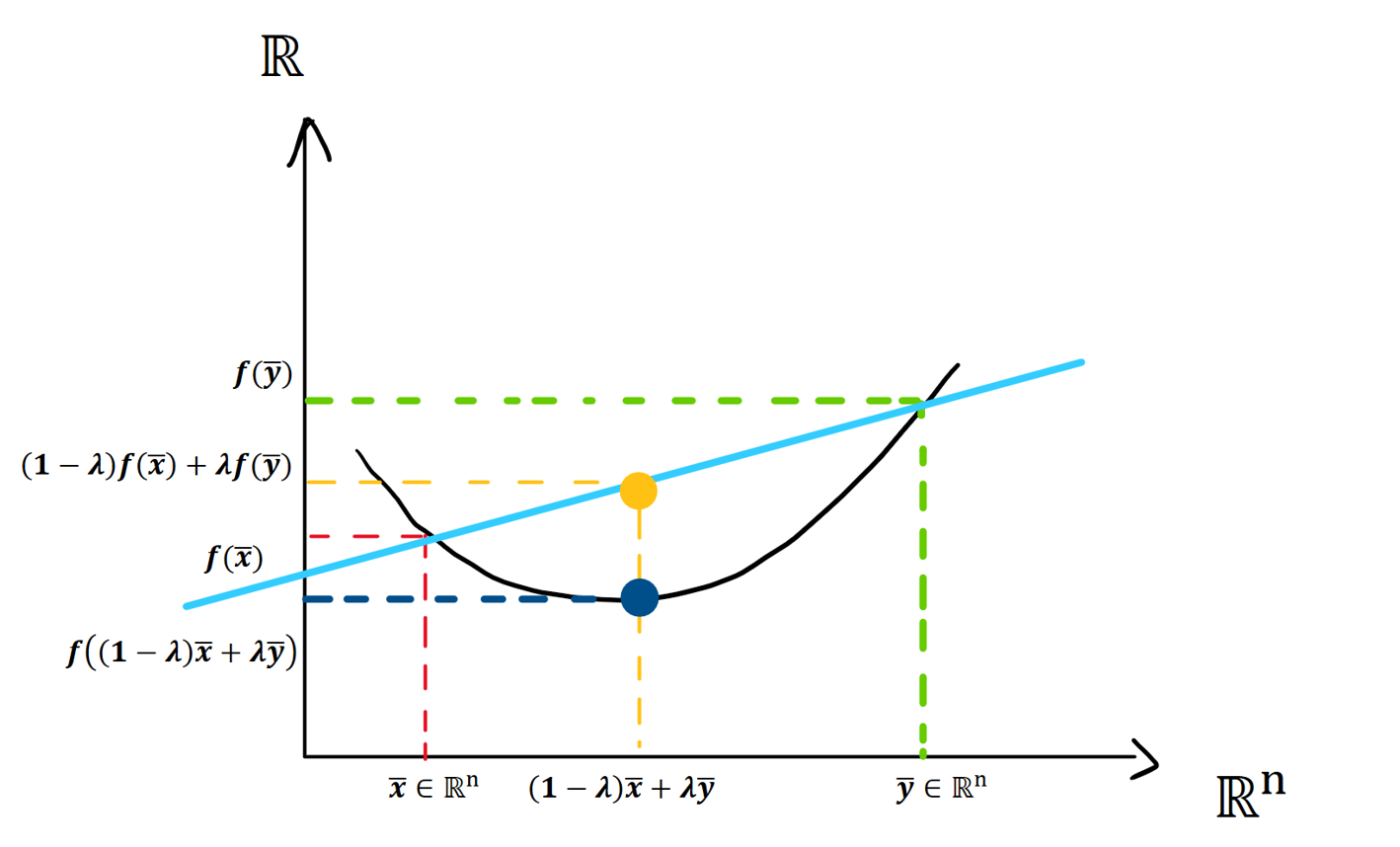
Definition: A function ${ f: \mathbb{R}^n \rightarrow \mathbb{R} }$ is called concave if for every pair of points ${ \bar{x}, \bar{y} \in \mathbb{R}^n }$ and every ${ \lambda \in [0,1] }$, we have
Affine functions
Can a function be both convex and concave?
Yes, consider this function ${ f: \mathbb{R}^n \rightarrow \mathbb{R} }$
And this form is called an affine function.
- Claim: Affine functions are both convex and concave.
Proof. suppose ${ f }$ is an affine function, that is there exist ${ \bar{c} }$ and ${ k }$ such that ${ \forall \bar{v} \in \mathbb{R}^n, f(\bar{v}) = \bar{c}^T \bar{v} + k }$
According to the definition of convex and concave function, our goal is to prove for every pair of ${ \bar{x}, \bar{y} \in \mathbb{R}^n }$, we have ${ \forall \lambda \in [0,1] }$
Let’s prove it,
QED.
- Claim. The converse is also true, that is, A function which is simultaneously convex and concave is necessarily an affine function.
Proof. Let $f:\mathbb{R}^n \rightarrow \mathbb{R}$ be a function, which is both convex and concave. Consider, the function $f:\mathbb{R}^n \rightarrow \mathbb{R}$ defined by
\[\begin{equation} g(\bar{t}) = f(\bar{t}) - f(\bar{0}) \nonumber \end{equation}\]Here, $\bar{t} = \left[\begin{matrix} t_1 \ t_2\ \vdots \ t_n \end{matrix}\right] \in \mathbb{R}^n,\bar{0} = \left[\begin{matrix} 0 \ 0\ \vdots \ 0 \end{matrix}\right] \in \mathbb{R}^n$
**Lemma 1: ** ${g(\bar{0}) = 0}$
From definition of $g$, we have
\[\begin{equation} g(\bar{0}) = f(\bar{0}) - f(\bar{0}) = 0 \end{equation}\]So, we get $g(\bar{0}) = 0$. Q.E.D.
**Lemma 2: ** function ${g}$ is both convex and concave
Proof. For any pair $\bar{x},\bar{y}\in \mathbb{R}^2$ , $\forall \lambda \in [0,1]$
\[\begin{equation} g((1-\lambda)\bar{x}+\lambda \bar{y}) = f((1-\lambda)\bar{x}+\lambda \bar{y}) - f\left( \bar{0}\right) \nonumber \end{equation}\]Because, $f(\bar{x})$ is both convex and concave, then we can get
\[\begin{equation} f((1-\lambda)\bar{x}+\lambda \bar{y}) = (1-\lambda)f(\bar{x}) + \lambda f(\bar{y}) \nonumber \end{equation}\]then we can get
\[\begin{equation} \begin{aligned} g((1-\lambda)\bar{x}+\lambda \bar{y}) &= f((1-\lambda)\bar{x}+\lambda \bar{y}) - f\left( \bar{0}\right) \\ & = (1-\lambda)f(\bar{x}) + \lambda f(\bar{y}) - f\left( \bar{0}\right) \\ & = (1-\lambda)\left(f(\bar{x})-f\left( \bar{0}\right)\right) + \lambda \left(f(\bar{y})-f\left( \bar{0}\right)\right) \\ & = (1-\lambda)g(\bar{x}) + \lambda g(\bar{y}) \end{aligned} \end{equation}\]Hence, $g(\bar{t})$ is also both convex and concave. Q.E.D.
Let’s denote $\bar{e_i} = \left[\begin{matrix} 0 & 0 & \cdots & 1& \cdots & 0 \end{matrix}\right]^\top \in \mathbb{R}^n, i \in {1,2,\cdots,n}$, where $i^{th}$ position is $1$.
**Lemma 3: ** ${\forall t_i \in \mathbb{R} }$, we have \(\begin{equation} g(t_i \cdot \bar{e_i}) = g(\bar{e_i}) \cdot t_i \end{equation}\)
Take $\bar{x} = \bar{0}, \bar{y} = \bar{e_i}$ and replace $\lambda$ as $t_i\in [0,1]$ in equation (8), we get
\[\begin{equation} g(t_i \cdot \bar{e_i}) = (1-t_i)\cdot g(\bar{0}) + t_i \cdot g(\bar{e_i}) \nonumber \end{equation}\]By Lemma 1, we have
\[\begin{equation} g(t_i \cdot \bar{e_i}) = t_i \cdot g(\bar{e_i}), \forall t_i \in [0,1] \end{equation}\]Take $\bar{x} = \bar{0}, \bar{y} = t_i \cdot \bar{e_i}$ and replace $\lambda \in (0,1]$ as $\frac{1}{t_i}, t_i\in [1,+\infty)$ in equation (8), we get
\[\begin{equation} g(t_i \cdot \bar{e_i}) = t_i \cdot g(\bar{e_i}), \forall t_i \in [1,+\infty) \end{equation}\]Combine formula (10) (11), we have
\[\begin{equation} g(t_i \cdot \bar{e_i}) = t_i \cdot g(\bar{e_i}), \forall t_i \in [0,+\infty) \end{equation}\]Take $\bar{x} = -t_i\cdot \bar{e_i}, \bar{y} = t_i \cdot \bar{e_i}, t_i \in \mathbb{R} $ and fix $\lambda = \frac{1}{2}$ in equation (8), we get
\[\begin{equation} g(-t_i \cdot \bar{e_i}) = - \cdot g( t_i \cdot \bar{e_i}), \forall t_i \in \mathbb{R} \end{equation}\]$\forall t_i \in (-\infty,0]$, that is $-t_i \in [0,+\infty)$, take $-t_i$ in formula (12), we have
\[\begin{equation} g(-t_i \cdot \bar{e_i}) = -t_i \cdot g(\bar{e_i}) \end{equation}\]From formula (13), we can get
\[\begin{equation} -t_i \cdot g(\bar{e_i}) = g(-t_i \cdot \bar{e_i}) = - g(t_i \cdot \bar{e_i}) \nonumber \end{equation}\]That is
\[\begin{equation} g(t_i \cdot \bar{e_i}) = -t_i \cdot g(\bar{e_i}), \forall t_i \in (-\infty,0] \end{equation}\]Combine formula (12) and (15), we have
\[\begin{equation} g(t_i \cdot \bar{e_i}) = t_i \cdot g(\bar{e_i}), \forall t_i \in \mathbb{R} \end{equation}\]Hence, we prove Lemma 3. Q.E.D.
**Lemma 4: ** ${g\left( \sum_{i=1}^n t_i \bar{e_i}\right) = \sum_{i=1}^n t_i g(\bar{e_i}) , \forall t_i \in \mathbb{R}, i \in {1,2,\cdots,n}}$
We will prove it by induction.
Base case is
\[\begin{equation} g(t_1 \cdot \bar{e_1}) = t_1 \cdot g(\bar{e_1}), \forall t_1 \in \mathbb{R} \nonumber \end{equation}\]it is correct by Lemma 3.
Induction Hypothesis: $g\left( \sum_{i=1}^k t_i \bar{e_i}\right) = \sum_{i=1}^k t_i g(\bar{e_i}) , k < n$ is correct
Let’s check $k=n$
Take $\bar{x} = 2 \cdot \sum_{i=1}^{n-1} t_i \bar{e_i}, \bar{y} = 2\cdot t_n\bar{e_n}$ and fix $\lambda = \frac{1}{2}$ in equation (8), we have
\[\begin{equation} g\left(\frac{1}{2}\cdot 2 \cdot\sum_{i=1}^{n-1} t_i \bar{e_i} + \frac{1}{2}\cdot 2\cdot t_n\bar{e_n}\right) = \frac{1}{2}\cdot g\left( 2 \cdot\sum_{i=1}^{n-1} t_i \bar{e_i}\right) + \frac{1}{2}\cdot g\left( 2\cdot t_n\bar{e_n}\right), \forall t_1 \in \mathbb{R} \nonumber \end{equation}\]By Lemma 3
\[\begin{equation} g\left(\frac{1}{2}\cdot 2 \cdot\sum_{i=1}^{n-1} t_i \bar{e_i} + \frac{1}{2}\cdot 2\cdot t_n\bar{e_n}\right) = g\left( \sum_{i=1}^{n-1} t_i \bar{e_i}\right) + g\left( t_n\bar{e_n}\right), \forall t_1 \in \mathbb{R} \nonumber \end{equation}\]By induction hypothesis,
\[\begin{equation} \begin{aligned} g\left(\frac{1}{2}\cdot 2 \cdot\sum_{i=1}^{n-1} t_i \bar{e_i} + \frac{1}{2}\cdot 2\cdot t_n\bar{e_n}\right) &= \sum_{i=1}^{n-1} t_i g(\bar{e_i}) + g\left(t_n \bar{e_n}\right) \\ &= \sum_{i=1}^{n} t_i g(\bar{e_i}), \forall t_1 \in \mathbb{R} \nonumber \end{aligned} \end{equation}\]Hence, we prove Lemma 4. Q.E.D.
**Lemma 5: ** ${g}$ is linear function
$\forall \bar{t} = \left[\begin{matrix} t_1 \ t_2\ \vdots \ t_n \end{matrix}\right] \in \mathbb{R}, t_i \in \mathbb{R}, i \in {1,\cdots,n}$, we can write $\bar{t}$ as $\sum_{i=1}^n t_i \bar{e_i}$. From Lemma 4,
\[\begin{equation} \begin{aligned} g(\bar{t}) &= \sum_{i=1}^{n} t_i g(\bar{e_i}) \\ & = [\begin{matrix} g(\bar{e_1}) & g(\bar{e_2})& \cdots & g(\bar{e_n}) \end{matrix}] \cdot \bar{t} \nonumber \end{aligned} \end{equation}\]Here, $g(\bar{e_i}=f(\bar{e_i}) - f(\bar{0}) \in \mathbb{R},i \in {1,\cdots,n}$. So, $g(\bar{t})$ is a linear function. Q.E.D
By definition of $g$, $f(\bar{t}) = g(\bar{t}) + f(\bar{0})$. By Lemma 5, $g$ is a linear function, we prove $f(\bar{t})$ is an affine function. $\square$