Last blog, we are talking about searching a pattern string in a text string. In fact, we treat the pattern string as a finite automaton which can jump to other position when we meet a mismatch. In this blog, we will consider a general case, that is find multiple pattern string in a text string. In specific, given a dictionary $D$ of $d$ words which has $m$ characters in total, we need to find all their occurrences in the text string $T$ with length $\vert T \vert = n$. If we employ KMP for each word in dictionary one-by-one, the total running time will be $\mathcal{O}(m+dn)$. In this blog, we will still use the idea similar as KMP, you will see the Trie and Aho-Algorithm in this blog.

Trie

Instead of directly talking about how to improve the running time of multiple-words searching. We first consider that how to quickly check if a word in given dictionary $D$. For example, ${D = \{\text{work},\text{worker}, \text{coworker}\}}$. We denote the query word $q$ with size of $n$, and the total character of dictionary is $m$. If we compare word $q$ to each of the word in $D$, the running time is $\mathcal{O}(nm)$. But now, we can construct a new data structure for for dictionary, called Trie. Basically, Trie is a tree, each edge represent a character and each node represent the prefix that is all the character in the path from root note to this node.

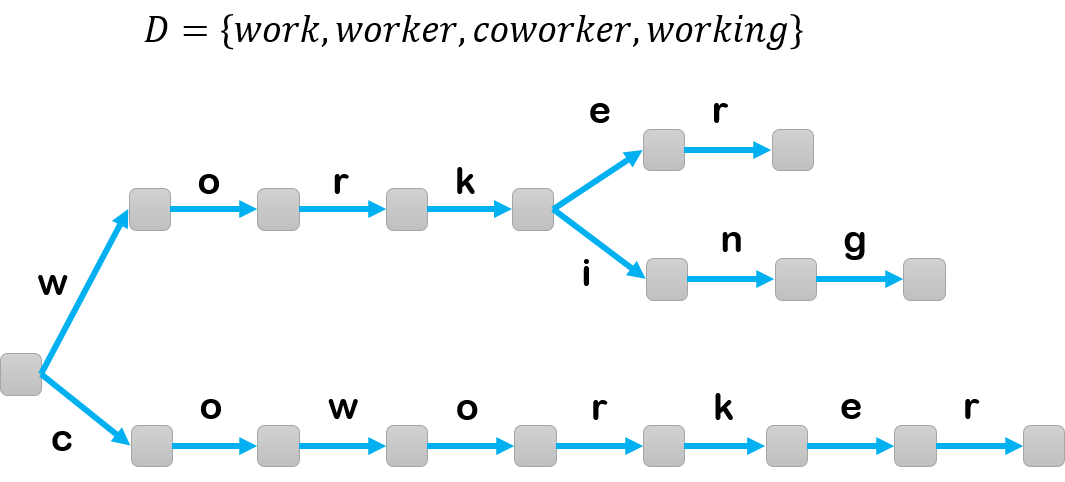
It’s easy to check that Trie can be constructed in $\mathcal{O}(m)$ time and space. (Note, for constructing, we take a word at each time, and check the character of the word one-by-one, if we don’t have this edge in the current tree, we add a new edge.) And the time of querying is $\mathcal{O}(n)$, where $n$ is the length of query word. (Note, in fact we take some time for checking the edge, because the size of alphabet for a string is a constant, so it’s still a linear time or we can use hash table to do it, the searching takes $\mathcal{O}(1)$).

Aho-Corasick algorithm

Now, let’s come back to the original problem. How to find multiple words in our text string. We can borrow the idea of KMP, we construct the dictionary as a Trie, and do some thing like prefix function, for each note we jump to the position with longest prefix in the Trie. This jump we called suffix link.

Suffix Link

We need go through all the vertices (we can take them as the order like BFS, because we need add the link level by level of the Trie)

• For the nodes in $2$nd level (these vertices contain only one letter), we always add suffix link going to the root.
• For other node $v$, we first check its parent node $p$ and jump to the node $w$, by the suffix link of $p$. And we try to check if there exists a child of $w$ match $v$ (in other word, if there has a character of an outgoing edge of $w$ matches the edge $(p,v)$’s representing character). If not, we jump to another node by suffix link of $w$ until we find a match or we add a suffix link to root.

The above figure show the suffix links in Trie. (Note we omit all the suffix link to root node)

Now, we try to analyze the running time of constructing suffix link. Define $\Pi(v)$ for each node $v$ in Trie, that means the level of the Trie (the distance from root to $v$). For each node,the number of comparisons does not exceed $\Pi(P(v))-\Pi(v)+2$, where $P(v)$ means the parent node of $v$ (For root node, $\Pi(r)=0$). So, the running time is summing them up for all nodes. But it’s hard to calculate, hence we estimate an upper bound, we define set $\text{PATH}$, which contains all the paths from root to leaves. Rather than all the nodes, we add one path at each time, that is

\[\sum_{v\in V} \Pi(P(v))-\Pi(v)+2 \leq 2 \vert V \vert + \sum_{P\in \text{PATH}} \left( \sum_{v \in P} \Pi(P(v))-\Pi(v) \right) = 2 \vert V \vert + \sum_{\ell \in L} \Pi(r) - \Pi(\ell) \leq 2\vert V \vert\]

where $L$ is the set of all the leaves of Trie. Hence, the suffix link can be constructed in linear time $\mathcal{O}(m)$ of nodes.

Running time of Aho-Corasick

Now come back to our original task, we want report all the occurrences of words in Text string $T$. We can still take the same idea like KMP. We move the pointer from $0$ to the end of $T$. Take an example, now we in position $i-1$, which corresponding to the node $v$ in dictionary Trie. Then, we move to $i$th position, and check if there exists a child of $v$ match the $i$th character of $T$. If not, we jump to another node by the suffix link of $v$ and keep going. So the running time is $\mathcal{O}(n)$, because we can consider the match segment is $[\ell,r]$ in $T$, if we extent matching we push $r$, otherwise, we use suffix link to jump we push $\ell$, so the running time is $\mathcal{O}(n)$. (In fact it’s not the running time of Aho-Corasick, we will talk it later)

But unlike KMP, how can we know there is a occurrence of word? If we only consider the situation that the some position in $T$ mapping to the leaves of Trie, we will find the word like “work” in above Trie will be ignored. So, we add a symbol $ for all the words in dictionary, like below.

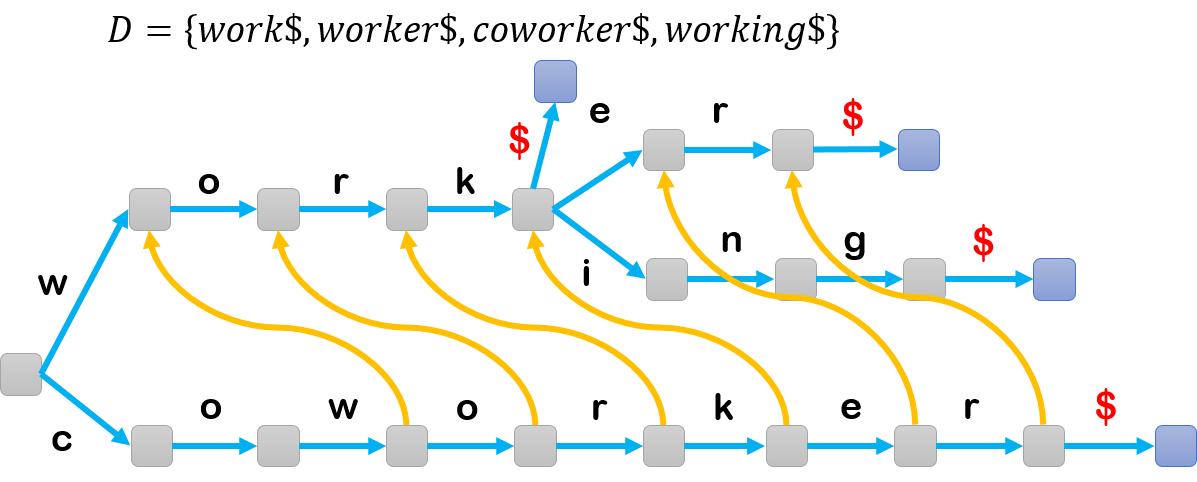
So, we need modify a little bit for the first description. At each step, when we finish the operation of $i$th position, we do extra check if we can add a $ after $i$th character. If it’s possible, we report that the occurrence of a word and move back (here we mean, we move from$ to original mapping node of $i$th character in Trie.) For example, we have the text $\textbf{abworkcd}$ and now we are at character $\textbf{r}$, and we know it mapping the node $v$ representing prefix $\textbf{wor}$, and we try to add a $ here, we don’t find any outgoing edge of node $v$ with symbol . Then we move forward at $\textbf{k}$, and we find we can keep going on Trie. Next, we ask again, if we can add $ here and we find there is an outgoing edge with $. So, we report occurrence of $\textbf{work}$ $. Then, we move back to node $\text{work}$ in Trie and move to next character $\textbf{c}$ in text. Hence, for above running time we need add the time we “move back” when we report an occurrence, that is $\mathcal{O}(m + R)$, where $R$ is the total number of occurrences of all words from dictionary.