At the beginning of our bioinformatic algorithms journal, we will focus on the similarity of strings. We we touch following aspects,
- Equality
- Find occurrences of string $S$ in a given string $T$.
- Edit distance
- Find edit distance between strings $S$ and $T$ (global alignment)
- Find substring of $T$ with minimal edit distance to given string $S$ (local alignment)
- Probability
- Construct probability model that best describes a given set of strings.
- Check if a given strings is likely to be of the same type.
Today, we will introduce the algorithm for first problem: find all occurrences of a string $P$ (called pattern string) in a given string $T$ as a substring.
Naïve algorithm
Given a pattern string $P$ and a text string $T$, we denote $m$ is the pattern size and $n$ is the text size ($m \leq n$). We can immediately get a naïve idea, that is we can slide text string $T$ with window size of $m$ from end to end. And check each substring with length $m$ if equals to pattern string $P$. Here is a pseudocode
1
2
3
4
5
6
7
8
9
NaïveMatch(P,T)
Occurrences = [] // record initial positions in T
for i = 0, 1, ..., n-m
j = 0
while j < m and P[j] = T[i+j]
j += 1
if j == m
Occurrences.append(i)
return Occurrences
It’s oblivious that the running time is $\mathcal{O}(mn)$. It’s not an efficient way, but we analyze it to see what happens and get some new idea.
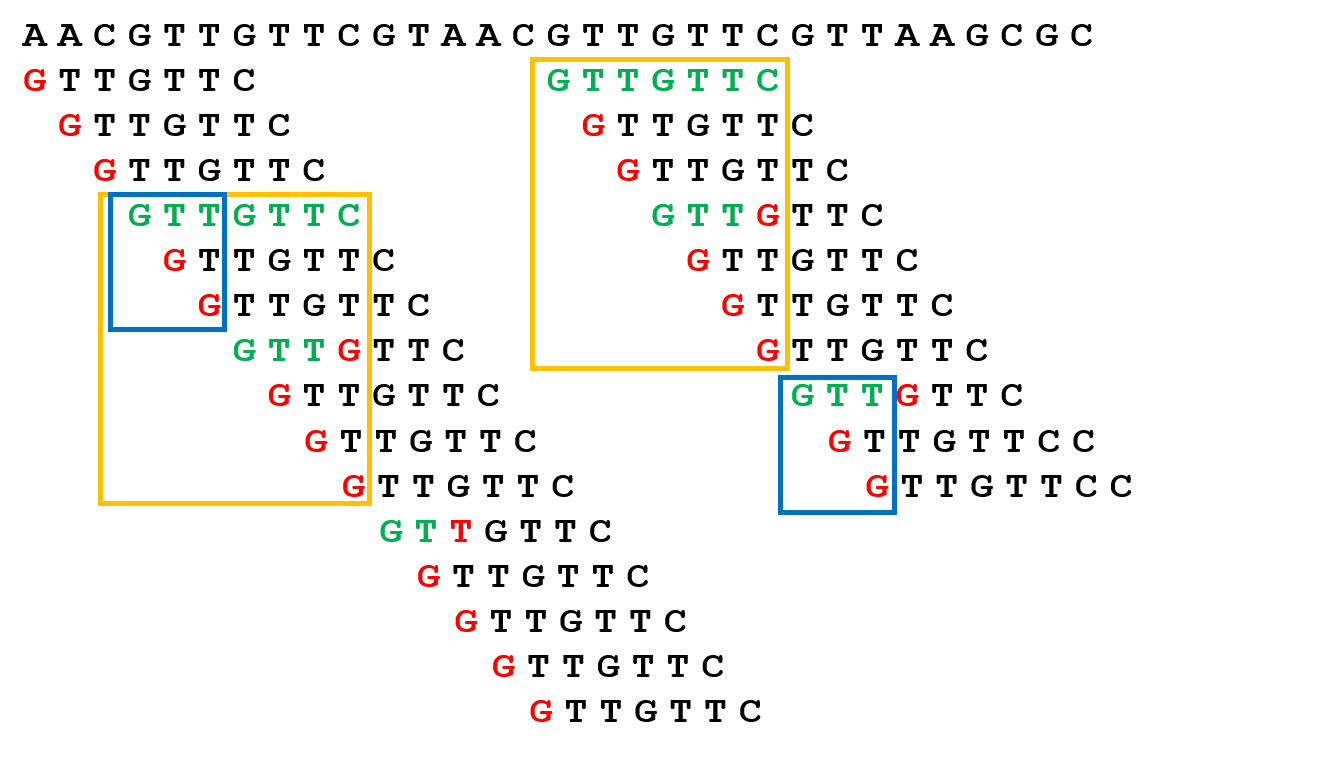
If you check the two yellow boxes in the figure, you will find the they have exactly the same content. It’s easy to get, because in this box we first get a match in $T$ and slide $P$ to try further alignments. So, the alignment pattern must be identical. Furthermore, if you check the blue box, it’s also identical. Because, given a prefix of $P$ denoted as $S$ including $P$ itself, the alignment result of suffix of $S$ and prefix of $S$ is identical. Hence, we get an idea, we don’t need to compute these alignment repeatedly. We can directly record these alignment and jump to next position that we don’t know. Okay, I know now it’s a little confusing for my description. I will give the algorithm as below and explain the key idea of the algorithm again.
Knuth-Morris-Pratt algorithm
Implement of KMP
Let’s specify our idea, image that we are going through a match substring of $T$ say $\text{G}_{i}\text{T}_{i+1} \text{T}_{i+2} \text{G}_{i+3} \text{T}_{i+4}$ (where the subscript represent the location in $T$), and then we find next character is not match. At that time, for the naïve idea, we will drop attempt this time, and start from $(i+1)^{\text{th}}$ location (next iteration of $i$ in naïve algorithm). But! If we already record the information of the yellow box in above figure. Let’s see what can be done? Because, we already know the alignment situation between the suffix of $\text{GTTGT}$ and each prefix of it. In the yellow box, we know the the prefix $\text{GT}$ match the suffix $\text{GT}$. So, we can directly move to the line that prefix $\text{GT}$ lies in. Because the middle process we already know and we just need to jump to the next match prefix which is a start for a possible match in $T$.
So, we can treat how KMP works as following way:
-
We calculate the yellow box for pattern string. In detail, for each character of $P$, we record the position of next green character in the same column, that is the length of prefix of next possible match. This array of function is called Prefix function $\Pi$.
-
We maintain a box that will enlarge when a new pair of match characters appears. If the next pair of characters is not match, we will drop this box and start a box according to the prefix function. (For above example $\text{GTTGT}$, $\Pi(4)=2$, the index of last $\text{T}$ is $4$ and the next match prefix is $\text{GT}$, which length is $2$.) Until the box increases to $m$ that means we find a substring in $T$ equal to $P$. And we also jump to next box by prefix function.
Let’s check the pseudocode
1
2
3
4
5
6
7
8
9
10
11
12
KMP(P,T)
Occurrences = [] // record initial positions in T
rs = 0 // length of the box
for i = 0, 1, ..., n-1
if P[rs] == T[i]
rs += 1
if rs == m
Occurences.append(i-m) // find a substring
while rs > 0 and (rs == m or P[rs] != T[i])
rs = Pi[rs] // jump to next box
// if rs = 0, and P[rs] != T[i], we don't have opearions in loop, that means we directly move to next loop.
return Occurrences
The running time for above pseudocode is $\mathcal{O}(n)$, which we will talk about later in the following section after introducing how to get prefix function. So, our next task is solving prefix function $\Pi$.
Prefix function
For any prefix $P[0…k-1]$ of string $P$ we calculate $\Pi(k)$ as its largest prefix matching its suffix: \(P[0\cdots\Pi(k)-1] = P[k-\Pi[k]\cdots k-1]\) Suppose $\Pi(k)$ is the largest prefix of $P[0\cdots k-1]$ that match its suffix.
- If $P[\Pi(k)] = P[k]$ that means the next character of prefix $P[0\cdots\Pi(k)-1]$ is equal to the next character of suffix $P[k-\Pi[k]\cdots k-1]$, then we can can record $\Pi(k+1) = \Pi(k) + 1$.
- If $P[\Pi(k)] \neq P[k]$ that means the next character of prefix $P[0\cdots\Pi(k)-1]$ is not equal to the next character of suffix, then we know $\Pi(k+1)$ will go back to a smaller suffix. So, what’s the possible suffix? No matter what, we need find a suffix/prefix like red region in following figure. Then, check if the next location of red prefix has identical character with $P[k]$ (the yellow square in figure). Okay, what’s the length red region? Oh!! That’s $\Pi(\Pi(k))$. Because $P[k-\Pi[k]\cdots k-1] = P[0\cdots\Pi(k)-1]$, so we find possible suffix (red region) in $P[k-\Pi[k]\cdots k-1]$ that equals to find possible suffix in $P[0\cdots\Pi(k)-1]$. And we know, the largest prefix in $P[0\cdots\Pi(k)-1]$ equals to suffix is $\Pi(\Pi(k))$.
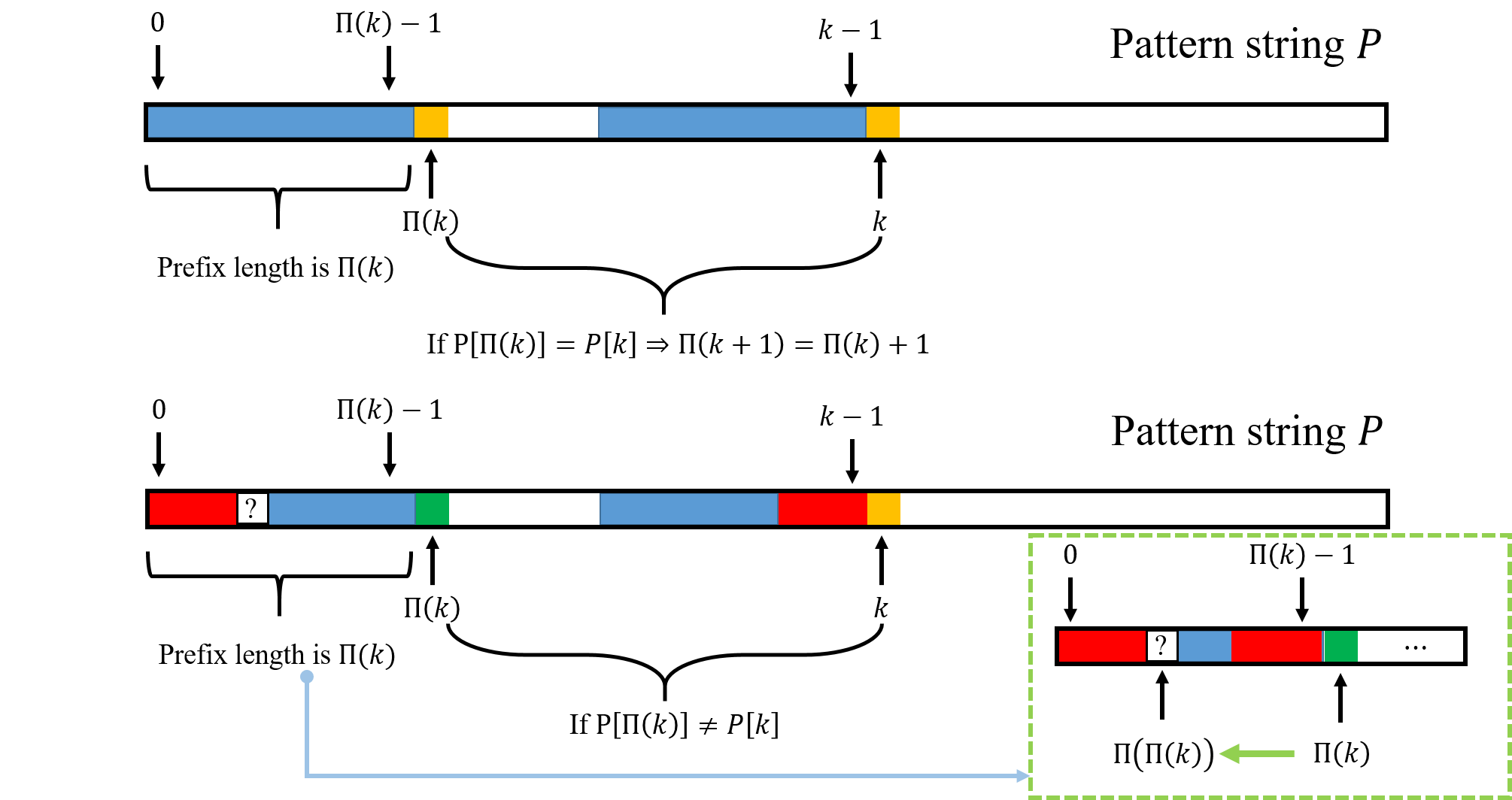
So the algorithm to calculating prefix function basically maintains the length of prefix, if match then enlarge, else jump to a smaller prefix (based on $\Pi$ function). Here, we give the pseudocode
1
2
3
4
5
6
7
8
9
10
11
PrefixFunction(P)
Pi[1] = 0
ps = 0 //Prefix size
for k = 1,2, ..., m-1
ps = Pi[k]
while ps > 0 and P[ps] != P[k]
ps = Pi[ps]
if P[ps] == P[i]
ps += 1
Pi[k+1] = ps
return Pi
Running Time Analysis
Basically, the running time of whole KMP and prefix function has same idea to analyze. First, we will show it in a more intuition way. Instead of paying attention to the index of loop, we focus on the interval $[\ell,r]$ that represent the matching suffix. If we find next character is match, we will push $r$ forward, otherwise we use prefix function to jump forward. But that means the left bound of matching suffix push forward, i.e. $\ell$. So, in each time we push $r$ or $\ell$ forward until the end of string. The total running time is $\mathcal{O}(n+m)$ for KMP or $\mathcal{O}(m)$ for prefix function.
Last, I will show it in a more rigorous way. Without loss of generality, we consider the process of prefix function. When we move from $k$th position to $k+1$th position, we have two case:
-
Next character is not matching, we need to jump to $\Pi(k),\Pi(\Pi(k)), \cdots$, what’s the upper bound? In fact, we stop at $\Pi(k+1)$, the we do at most $\Pi(k)-\Pi(k+1)+1$ jumps and we do once comparisons when we first find next character is not matching. Hence, the total number of comparisons at this position is at most $\Pi(k) - \Pi(k+1) + 2$.
-
Next character is matching, so we only do once comparison. And we know $\Pi(k+1) = \Pi(k) + 1$. We can also write it as $\Pi(k) - \Pi(k+1) + 2$
Hence, the total running time is $\sum_{k=0}^{m-1} \Pi(k) - \Pi(k+1) + 2 = 2m+ \Pi(0) - \Pi(m-1) = \mathcal{O}(m)$.
LazyKMP
In fact, the idea of how to get prefix function/array can inspire us to find another way to find pattern string $P$ in text $T$. In fact, we can construct a string like $P \& T$. Because the $\&$ symbol separates the string $P$ and $T$, the length of matching prefix at most as long as $\vert P \vert$. Hence we can get a longer array $\Pi$ for whole $P\&T$, when we go through each location in $T$, we calculate $\Pi(k)$, which corresponding to a prefix of $P$ (because any suffix cannot match up to $\&$). If some location $k$ has $\Pi(k) = m$, then we know there is a substring of $T$ equals to $P$.
1
2
3
4
5
6
7
LazyKMP(P)
Pi = PrefixFunction(P&T)
Occurrences = [] // record initial positions in T
for i = m+1 ... n-1
if Pi[i] == m
Occurrences.append(i-m-m)
return Occurrences
In fact, LazyKMP has same running time with original KMP, but with high space complexity ($\mathcal{O}(n+m)$). Because $\Pi$ don’t need to store all the longest prefix of all the positions.
Z-function
We define “Z-function” $z$ as follow:
For position $k$ in a string $T$, we define $z(k)$ is the longest substring of $T$ starting in position $k$ that matches a prefix of $T$.
Off course, we can get a naïve algorithm to compute Z-function, for each position $i$, do one-by-one check for $T$’s prefix. We know the running time is $\mathcal{O}(n^2)$ (suppose $\vert T \vert = n$). Can we do thing like the idea of prefix function? Yes!
Suppose $T[\ell\cdots r]$ is the rightmost match segment (match to prefix $T[0 \cdots r-\ell]$) we know currently. Know we want the compute $z(i), i\geq \ell$, and we already know the value of $z(1),z(2),\cdots,z(\ell-1)$.
-
Case 1: If $i > r$, this is out of scope of our known pattern of $T$, we have to explore it. That is we need to one-by-one check for the prefix of $T$ and $T[i\cdots n-1]$. Until we find the longest matching prefix, we stop and return $z(i)$. And now, we can update the rightmost match segment, $\ell = i, r = i + z(i) - 1$.
-
Case 2: If $i \leq r$, we know $i$ drop in the interval $[\ell,r]$. We know $T[\ell \cdots r] = T[0\cdots r- \ell]$, so we can consider position $i-\ell$ which is the corresponding position of $i$ in prefix $T[0\cdots r- \ell]$. We know the largest prefix for position $i-\ell$ is $z(i-\ell)$.
- If $z(i-\ell) \leq r-i+1$, we know $z(i-\ell) = z(i)$, because the extension of $i-\ell$ stop before position $r-\ell$. At this situation, we don’t need to update $r,\ell$.
- Otherwise, we know the prefix of $i$ is at least $r-i+1$, and still has the potential to extend. We need do one-by-one check to push $r$ forward. Then we stop when the first mismatch appears, and record $z(i)$. In the end, we still update $\ell = i, r = i + z(i) - 1$.
Here we give the pseudocode formally
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Z-Function(T)
l, r = 0, 0
z = [0]*n
for i = 0, 1, ..., n-1
if i <= r and z[i-l] <= r - i + 1
z[i] = z[i-l]
else
z[i] = max(0,r-i+1)
while i + z[i] < n and T[z[i]] == T[i + z[i]]
z[i] += 1
if i + z[i] - 1 > r
l = i
r = i + z[i] - 1
return z
We can trace the behavior of updating $r$, which increases from $0$ to $n-1$ and the other part is apparently $\mathcal{O}(n)$, so the total running time is $\mathcal{O}(n)$.
Z-Algorithm
We find Z-function are quite similar with prefix function, they are basically symmetric process. So, we can design another algorithm called Z-algorithm to find pattern string $P$ in text string $T$ like LazyKMP. In specific, we construct string $P\&T$ and calculate Z-function for the new string, because there any segment start from any position in $T$ cannot find a match prefix overcoming $\&$.
1
2
3
4
5
6
7
LazyKMP(P)
z = Z-Function(P&T)
Occurrences = [] // record initial positions in T
for i = m+1 ... n-1
if Pi[i] == m
Occurrences.append(i-m)
return Occurrences
It’s obviously, the time complexity and space complexity both are $\mathcal{O}(n+m)$.