今天介绍一篇还未正式发布,公布在bioRxiv上的文章,是一个全新的生物信息学问题,关于冠状病毒的转录组拼接. 我个人而言,非常喜欢这项工作,完全从一个实际的生物学问题出发,然后构建严谨的数学模型,每一步都有数学推导,没有玄学的地方,为了求解模型,利用各种性质进行简化、变形. 最终的结果也非常优秀. 下面与诸君奇文共赏!
Background
Nidovirales(巢病毒目)的病毒基因通过独立的RNA聚合酶,采用一种不连续的转录本来进行方式,这个过程不同于可变剪接. 这个“目”的病毒包含一条单链RNA(正义链,大约30kb,是比较大的病毒基因组了),靠近${ 5‘ }$端的序列编码非结构蛋白,靠近${ 3‘ }$端的序列编码结构蛋白和附属蛋白. 所谓结构蛋白就是,病毒颗粒的组成成分(比如包膜蛋白,刺突蛋白、膜蛋白、核壳蛋白);非结构蛋白主要是负责病毒的RNA复制所需.
听起来很复杂,其实知道了病毒的生活史之后,还是挺简明的,我们都知道病毒需要寄生在细胞内才能生活,在外界游离的时候,只带了遗传物质和结构蛋白,等进入宿主细胞后,因为其遗传物质是RNA,而且和真和生物的mRNA一样,有${ 5‘ }$端帽子和${ 3‘ }$端ploy-A尾巴,所以${ 5‘ }$端的序列被宿主的核糖体翻译为蛋白质. 其中有一种pp1ab的蛋白质,翻译后被切割成十多种非结构蛋白(非结构蛋白从pp1a切割而来),这些非结构蛋白主要负责RNA的复制,也有些负责抑制宿主的mRNA转录和免疫等等. 组装的时候,只组装结构蛋白,再次释放到外界. 辅助蛋白有一些是为了抵抗宿主的免疫反应,还有很多功能暂不清楚.
具体的,非结构蛋白区域表达一种称为RNA-dependent RNA polymerase(RdRp)的复合物. RdRp是一种转录复合物,在转录的时候会跳过一些病毒RNA模板上的基因序列(segment). 这个过程称为discontinuous transcripts,如Fig.1所示,而我们的任务是组装完整的转录本集合${\mathcal{T}}$ 还有丰度${\mathcal{c}}$.
如果我来总结一下,巢病毒转录本的拼接和真核生物可变剪接的区别,我觉得主要是真核生物的转录本,虽然是可变剪接,但是剪接位点基本是固定的,但是巢病毒不是;同时巢病毒的两侧序列基本是固定的,而真核生物不一定.
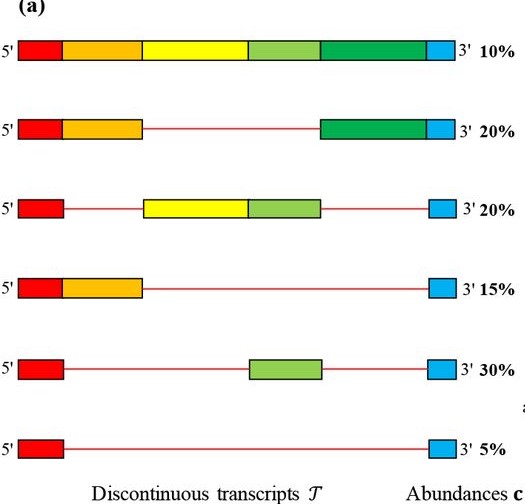
Fig.1 Discontinuous transcripts1.
在这篇文章,作者提出了${\Large D}$ISCONTINUOUS ${\Large T}$RANSCRIPT ${\Large A}$SSEMBLY问题,给定测序片段在参考基因组上的比对结果${\mathcal{R}}$,然后寻找转录本集合${\mathcal{T}}$ 还有丰度${\mathcal{c}}$. 如下图Fig.2所示.
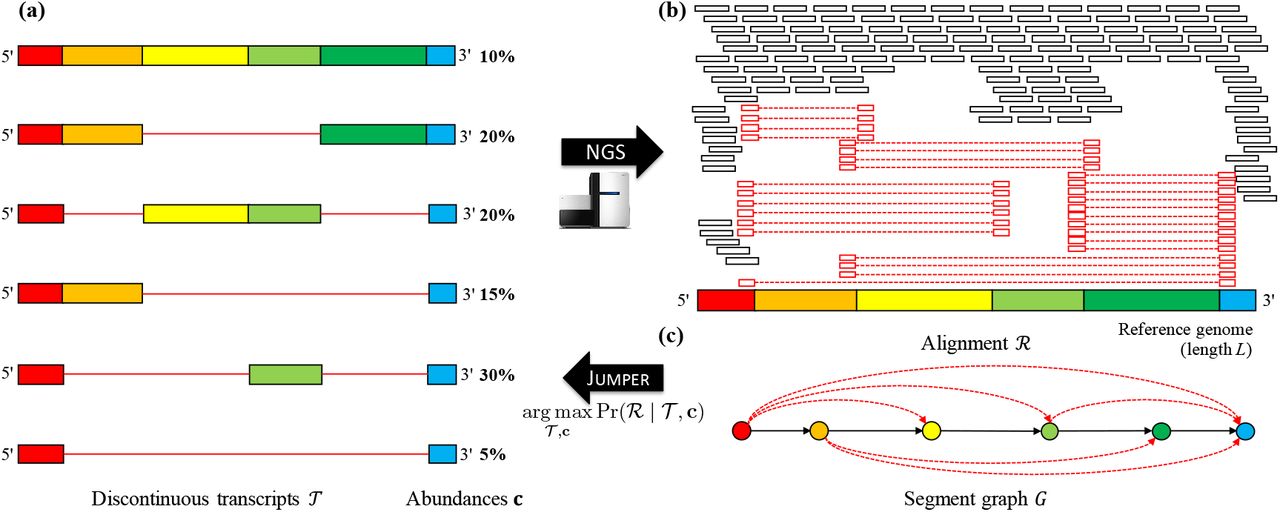
Fig.2 DISCONTINUOUS TRANSCRIPT ASSEMBLY problem1.
Preliminaries and Problem Statement
Def.1 给定参考基因组,那么定义discontinuous transcript ${T=v_1,\cdots ,v_{|T|}}$,(i)其中${v_i}$是参考基因组上一段连续的区域; (ii)segment ${v_i}$ 一定在参考基因组上的位置先于${v_{i+1}}$,${i\in {1,\cdots , \lvert T \rvert-1}}$; (iii)${v_1}$包含${5’}$端的序列,${v_{\lvert T \rvert}}$包含${3’}$端的序列.
在文献中,discontinuous transcripts被称为subgenomic transcripts,或者subgenomic RNAs(sgRNA). 转录本集合${\mathcal{T}={T_i}}$和对应的丰度${\mathcal{c}=[c_i],c_{i} > 0}$,并且${\sum_{i=1}^{\lvert \mathcal{T} \rvert} c_i =1}$. 文章使用类似STAR这样的splice-aware的比对软件进行比对.
文章提出了一种称为${segment \ graph \ G}$的图. 具体而言,每一个phasing read(比对到的区域不连续),会被参考基因组上的两个位置${v,w (w-v\geq 2)}$分离,这些位置称为${junctions}$,如果phasing read ${r\in \mathcal{R}}$比对到了${q \geq 2}$个不同的区域,那么就会产生${2q-2}$个junctions,我们把所有phasing read产生的junctions以及${1,L}$这两个位置放在一起,我们将参考基因组划分成一些闭区间${[v^-,v^+]}$(区间内不含有别的junction),这些区间(segments)就是图${G}$的顶点集${V}$了,我们定义边集${E^{\rightarrow}}$为连续的边集合,${E^{\curvearrowright}}$为不连续边集合,也就是${E^{\rightarrow}}$表示在参考基因组上连续的两个segment的连边,而${E^{\curvearrowright}}$表示在phasing reads ${\mathcal{R}}$上邻接的segment(至少有一个phasing read支持). 上述过程,如Fig.3示意.
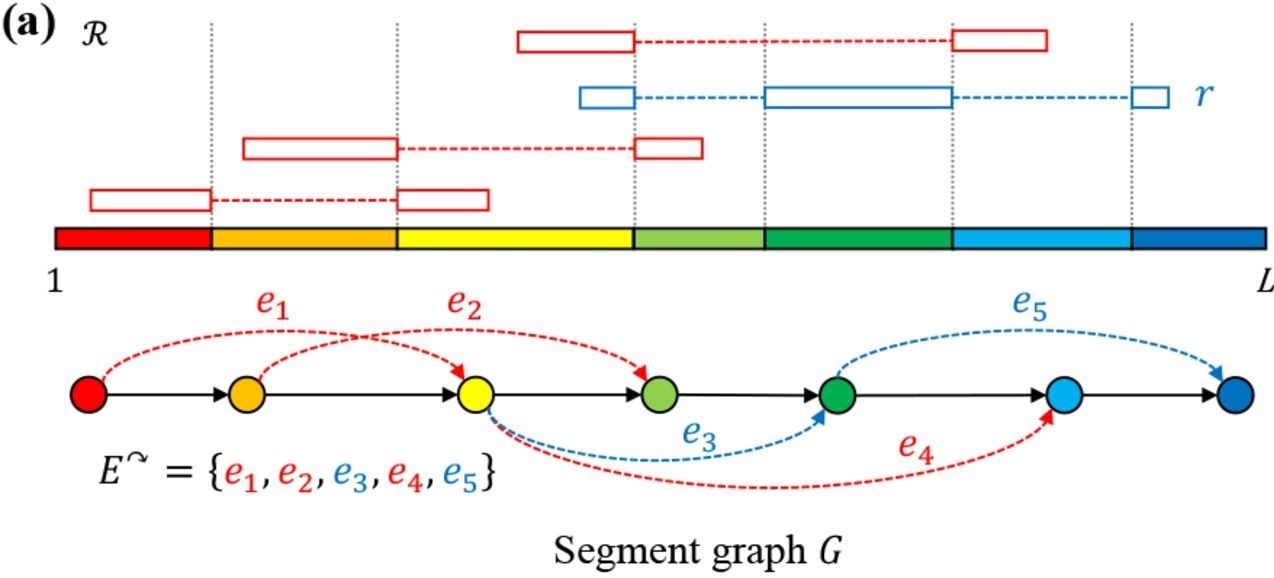
Fig.3 Segment Graph1.
Def.2 给定一个比对${\mathcal{R}}$,对应的${segment \ graph \ G = (V,E^{\rightarrow}\cup E^{\curvearrowright})}$是一个有向图,定点集合${V}$是segments的集合,边集${ E=E^{\rightarrow}\cup E^{\curvearrowright} }$由两种边${(v=[v^-,v^+],w=[w^-,w^+])}$组成,一种是连续的,即${v^+=w^-}$,或者不连续的,即${w^- - v^+ \geq 2}$,且存在phasing read使得${v^+}$和${w^-}$邻接.
Observation.1 Segement graph是一个有向图无圈图(有向圈),而且存在唯一一条Hamiltonian path.
唯一的哈密顿路就是${ E^{\rightarrow} }$,因为discontinuous transcript中的Segment都是按照再参考基因组上的位置排列的,所以不可能出现哈密顿路. 因此${ E^{\rightarrow} }$是唯一的哈密顿路. 因此,${G}$也只包含唯一的源点和汇点${s,t}$,而且每个discontinuous transcript都对应一条${ s-t }$ path ${\pi(T)}$.
PS: splice graph也是有向无圈图,大部分的情况也是唯一的源点、汇点,但是不一定存在哈密顿路.
我们的目标是就是极大化下面的后验概率
根据贝叶斯公式,我们要最大化前面的概率,就等价于优化后面这个式子,在假设没有别的信息的情况下,先验概率${ Pr(\mathcal{T},\mathcal{c}) }$是一样的,所以我们的优化目标就是${ Pr(\mathcal{R} \mid \mathcal{T},\mathcal{c}) }$. 下面我们来推导给定转录本集合${\mathcal{T}}$和丰度${\mathcal{c}}$的情况下,观察到比对结果${\mathcal{R}}$的概率.
令${ \mathcal{R} }$是reads的集合${ {r_1,\cdots, r_n} }$,转录本集合${ \mathcal{T} = {T_1,\cdots,T_k} }$ 以及相应的长度${L_1,\cdots, L_k}$,以及丰度 ${ \mathcal{c} = [c_1,\cdots,c_k] }$. 然后,我们假设read的长度是固定的${ \ell }$,因此
此处,${ Z_{i,j} }$是指示随机变量,表示事件${ T_i }$是read${ r_j }$的原始转录本. 其中${ Pr(Z_{i,j} \mid \mathcal{T},\mathcal{c}) }$表示转录本${ T_i }$产生read的概率,为(通俗而言,碱基的数量占比)
而${ Pr(r_j \mid Z_{i,j}) }$表示${ T_i }$生成${ r_j }$的概率,如下,如果${ T_i }$对应的path包含${ r_j }$对应的path,那么概率就是${ 1/L’_i }$其中${ (L’_i = L-\ell) }$,因为read长度固定,概率取决于初始位置.
因为我们假设转录本的长度远远长于read的长度${ L \gg \ell }$,所以${ L’_i / L_i \approx 1 }$. 因此我们可以进行推导
Problem 1 (${\Large D}$ISCONTINUOUS ${\Large T}$RANSCRIPT ${\Large A}$SSEMBLY(DTA)). 给定alignment ${ \mathcal{R} }$和整数${ k }$,寻找discontinuous transcripts ${ \mathcal{T} = {T_1,\cdots,T_k} }$和丰度${ \mathcal{c} = [c_1,\cdots,c_k] }$满足
(i)每个${ T_i \in \mathcal{T} }$是${ s-t }$ path.
(ii)${ Pr(\mathcal{R} \mid \mathcal{T},\mathcal{c}) }$极大.
Combinatorial Characterization of Solutions
下面我们利用Segment graph上的性质,来简化上面的问题
Def.3 Segment Graph ${ G }$的两个边${ (v=[v^-,v^+],w=[w^-,w^+]) }$和${ (x=[x^-,x^+],y=[y^-,y^+]) }$有overlap定义为开区间${ (v^+,w^-) }$和${ (x^+,y^-) }$有交集,即${ (v^+,w^-)\cap (x^+,y^-) \ne \emptyset }$.
那么对于任何转录本${ T }$,其对应${ G }$的一条${ s-t }$ path,如果我们只给定${ T }$的discontinuous edges ${ \sigma(T) }$,那么其中${ T }$的continuous edges会被${ \sigma(T) }$和${ G }$唯一确定. 反之,给定了${ T }$的路径${ \pi(T) }$,discontinuous edges ${ \sigma(T) =\pi(T) \cap E^{\curvearrowright} }$,也被唯一确定.
Propostions 1. 两两之间互不overlapping的discontinuous edges集合所形成的集族,和所有的${ s-t }$ path集合之间构成双射.
Proof:
设所有的${ s-t }$ path的集合为${ \Pi }$,${ \Sigma }$是pairwise non-overlapping(内部边两两不交的)${ E^{\curvearrowright} }$的子集构成的集族. 我们可以证明${ \Pi }$和${ \Sigma }$之间是双射.
道理也很简单,给定${ s-t }$ path ${ \pi \in \Pi }$,我们抓取其所有的discontinuous edges,就可以形成一个pairwise non-overlapping disconnected edges集合.
反之,给定一个pairwise non-overlapping disconnected edges ${ \sigma \in \Sigma }$,我们可以唯一确定continuous edges,然后合并起来就是${ s-t }$ path. ${ \square }$Def.4 我们将每个read ${ r }$刻画为一个集合对${(\sigma^{\oplus}(r),\sigma^{\ominus}(r))}$,称为disconnected edges的特征,其中${ \sigma^{\oplus}(r) }$表示read ${ r }$中的dicontinuous edges,即${ \sigma^{\oplus}(r) = \pi(r) \cap E^{\curvearrowright} }$. ${ \sigma^{\ominus}(r) }$表示dicontinuous edges的集合,其中的边${ (v=[v^-,v^+],w=[w^-,w^+]) \in E^{\curvearrowright} \backslash \sigma^{\oplus}(r)}$,且与${ \pi(r) }$中的一条边有overlap.
Propostions 2. 令${ G }$是Segment graph,${ T }$是转录本,${ r }$是read. 那么${ \pi(T) \supseteq \pi(r) }$当且仅当,${ \sigma(T)\supseteq \sigma^{\oplus}(r) }$且${ \sigma(T)\cap \sigma^{\ominus}(r) = \emptyset}$.
Proof:
首先说明充分性${ \Rightarrow }$,比较容易.
因为,${ \pi(T) \supseteq \pi(r) }$,所以${ \sigma(T) \supseteq \sigma^{\oplus}(r) }$,同时因为${ \pi(T) \supseteq \pi(r) }$ ,所以与${ \pi(r) }$有overlap的dicontinuous edges,必然也与${\pi(T) }$存在overlap. 又因为${ \pi(T) }$是${ s-t }$ path,所以其内部的边不存在overlap,所以${ \sigma^{\ominus}(r) }$与${ \pi(T) }$没有交集,否则${ \pi(T) }$内部出现ovelap,因此${ \sigma(T)\cap \sigma^{\ominus}(r) = \emptyset}$.
再来看必要性${ \Leftarrow }$,略微有些复杂.
根据条件${ \sigma(T)\supseteq \sigma^{\oplus}(r) }$,我们可以得到${\pi(T) \cap E^{\curvearrowright} = \sigma(T) \supseteq \sigma^{\oplus}(r) = \pi(r) \cap E^{\curvearrowright}}$.
再根据条件,${ \sigma(T)\cap \sigma^{\ominus}(r) = \emptyset}$,这意味着${ \sigma(T) }$的所有边都与${ \pi(r) }$的所有边不重叠,我们已经知道${ \pi(T) }$是${ s-t }$ path,且包含了${ \pi(r) }$所有的dicontinuous edges. 我们现在梳理一下,${ \sigma(T) }$与${ \pi(r) }$的边完全不overlap,那么也就是说,与${ \pi(r) }$中的continuous edges完全不overlap,我们知道,${ T }$是${ s-t }$ path,那么你想和${ \sigma(T) }$完全不相交,只能落在${ \pi(T) }$的continuous edges里面,所以,${ \pi(T)\cap E^{\rightarrow} \supseteq \pi(r)\cap E^{\rightarrow}}$.
由此,我们可得,${ \pi(T)\supseteq \pi(r) }$. ${ \square }$所以,我们可以将上述的公式(11),化为下面的式子
其中集合${ X(\mathcal{T},\sigma^{\oplus}_j,\sigma^{\ominus}_j) }$中的元素${ T_i\in\mathcal{T} }$其满足 ${ \sigma(T_i)\supseteq \sigma^{\oplus}_j }$且${ \sigma(T_i)\cap \sigma^{\ominus}_j = \emptyset}$.
注意到,此时我们已经将判断read ${ r }$在转录本${ T }$中的问题,归结为了图中的边的overlap的问题.
Methods
规划问题的变形处理
令${ S={(\sigma_1^{\oplus},\sigma_1^{\ominus}),\cdots,(\sigma_m^{\oplus},\sigma_m^{\ominus})} }$是所有read产生的边集合对,因为有一些不同的read会对应相同的Segment上的path,所以${ S }$集合的大小是${ m }$,然后我们令${ d={d_1,\cdots,d_k} }$表示reads对应到上面这些${ S }$中边集合对的个数. 所以,我们进一步改写式子(12),如下
然后我们对于上式取log
所以下面给出我们的数学规划
我们为了消去第二项,给出下面的引理
Lemma 1. 令${ D>0 }$是一个常量,${ \overline{c}_ i (c) = c_i D / \sum_{j=1}^k c_j L_j}$,和${c_i (\overline{c}) = \overline{c}_ i / \sum_{j=1}^k \overline{c}_ j \ ,\forall i\in [k]}$. 那么${( \mathcal{T},c = [c_1(\overline{c}),\cdots,c_k(\overline{c})]) }$是上述数学规划(18)-(21)的最优解,当且仅当${ (\mathcal{T},\overline{c} = [\overline{c}_ 1(c),\cdots,\overline{c}_ k(c)]) }$是下面数学规划的最优解
关于这个Lemma的证明,我放在了文章最后的附录中.
约束条件的数学刻画
转录本的组成
我们前面已经知道,转录本${ T }$可以由${ \sigma(T) }$唯一的表示,所以我们的条件约束${ (23) }$,即转录本必须是${ G }$中的${ s-t }$ path,换言之,我们只需要选择一些不overlap的discontinuous edges就可以了. 因此,引入二元变量${ x= { 0,1 }^{\lvert E^{\curvearrowright} \rvert \times k}}$,表示某个discontinuous edge是否在某个转录本中,对于discontinuous edge ${ e=(v=[v^-,v^+],w=[w^-,w^+]) }$,令${ I(e) }$表示Segment ${ v,w }$之间的开区间${ (v^+,w^-) }$. 根据Propostions 1,我们知道,如果两个不同的边${ e,e’ }$存在于同一个转录本,则${ I(e)\cap I(e’) = \emptyset }$. 所以
什么意思呢,就是如果两个不同的discontinuous edge存在overlap,则不能出现在同一个转录本中.
转录本丰度和长度
我们令${ D=\ell^* }$,其中${ \ell^* }$表示${ G }$中最短的${ s-t }$ path,所以规划中的约束改为${ \sum_{i=1}^k c_i L_i = \ell^* }$. 此时${ c_i L_i \leq \sum_{j=1}^k c_j L_j = \ell^* }$,且${ L_i \leq \ell^* }$,所以${ c_i \leq 1 }$.
对于某个discontinuous edge ${ e=(v=[v^-,v^+],w=[w^-,w^+]) }$,令${ L(e)=w^- - v^+ }$表示间隔的开区间的长度,那么我们可以想到,转录本的长度可以表示为基因组的长度${ L }$减去discontinuous edges跨过的区间长,即
然后我们引入连续变量${ z_e \in [0,1]^k }$,并且通过下面的约束${ z_{e,i} }$使其满足${ z_{e,i} = c_i x_{e,i} }$.
可以发现,当${ x_{e,i} = 0}$时候,${ z_{e,i} = 0 }$;当${ x_{e,i} = 1}$时,${ z_{e,i} = c_i}$. 没有问题.
所以,约束条件${ \sum_{i=1}^k c_i L_i = \ell^* }$,表示如下
最终结果如下,其中不涉及转录本的长度${ L_i }$
不连续边的特征${ (\sigma^{\oplus}_j,\sigma^{\ominus}_j) }$
在目标函数中,${ d_j }$是已知常数,我们现在将引入非负的连续变量${ q= {q_1,\cdots,q_m} }$来替代${ \log \sum_{i\in X(\mathcal{T},\sigma^{\oplus}_j,\sigma^{\ominus}_j)} \mathcal{c} _i }$,我们回忆Propositions 2,可以得到下面的等式(也就是,${ \sigma_j^{\oplus} }$中的边都属于转录本${ T_i }$,${ \sigma_j^{\ominus} }$的元素都不属于转录本${ T_i }$)
进一步我们引入连续变量${ y_j \in [0,1]^k }$来替代${ c_i \prod_{e\in \sigma_j^{\oplus}} x_{e,i} \prod_{e’\in \sigma_j^{\ominus}} x_{e’,i} }$,这个${ y_{j,i} }$恰好代表了不连续边特征${ (\sigma^{\oplus}_ j,\sigma^{\ominus}_ j) }$对于转录本${ T_i }$的贡献. 所以我们将${ c_i \prod_{e\in \sigma_ j^{\oplus}} x_{e,i} \prod_{e’\in \sigma_ j^{\ominus}} x_{e’,i} }$重新可化为下面的约束
同样,很容易验证,如果${ (\sigma^{\oplus}_ j,\sigma^{\ominus}_ j) }$其刻画的dicontinuous edges真的属于${ T_i }$,则${ y_{j,i} = c_i}$,否则,${ y_{j,i} = 0 }$. 因此我们得到了
目标方程
根据上一小节的描述,现在的目标方程改为了
我们使用lambda method来近似目标函数,首先将定义域${ (0,1] }$分成${ h }$个断点${ b_1 \leq b_2 \leq \cdots \leq b_h }$,然后引入变量${ \lambda_j \in [0,1]^k }$,并进行约束
然后${ \forall j\in [m] }$,${ \log }$函数近似为
这里为什么如此近似,我也不是非常的清楚,参考文献41有进一步的介绍,但是文章太数学了,并没有非常清楚,大意就是如何将这种convex (or concave) function近似成分段线性函数,来求最优值;我个人觉得首先${ q_j }$是对于${ b_1,\cdots,b_h }$的一个凸组合,然后下面的这个近似的形式非常像Jensen不等式,也许当我们插入很多的点也许就能非常接近${ q_j }$此处的函数值${ \log q_j }$.
注意到${ \log(b_o) }$都是一些常数. 所以,现在我们将${ \log }$函数转化为了线性的问题,即我们最大化下面问题
下面我们考虑另一个问题,因为我们选择对于似然函数取${ \log }$,这就意味着${ q_j }$必须大于零,我们回过头看${ q_j }$的原始定义${ q_j = \sum_{i=1}^k \left(c_i \prod_{e\in \sigma_j^{\oplus}} x_{e,i} \prod_{e’\in \sigma_j^{\ominus}} x_{e’,i}\right) }$,这意味着至少一个${ (\sigma_j^{\oplus},\sigma_j^{\ominus}) }$所刻画的path要属于${ T_i }$,否则整个式子无法计算. 这样的话,有一些read如果出错的话,我们将不得不考虑,且无法排除. 所以我们修改目标函数,做如下处理,首先引入新的断点${ b_0 = 0 }$,那么仍然满足
目标函数引入一个非常小的常量${ \delta }$,改为
这篇文章令${ \delta = b_1 /100 = 1/( 2^{h-1} \times 100) }$,${ h }$留给用户选择. 关于如何选择breakpoint,其实有很多讲究,也在参考文献41中,这篇文章选了最简单的方式,${ b_i = 2^{i-1} / 2^{h-1} }$,然后${ b_1 = 1/2^{h-1} ,b_h = 1 }$.
综上,我们终于得到了最终的规划的形式,如下Fig.4
Fig.4 Final Programming1.
步进启发式算法
下面我们来看,文章是怎么求解规划的,首先输入的是${ \mathcal{R} }$和整数${ k }$,其表示最大的转录本数目. 第${ p }$次迭代的时候,我们输入之前累积的${ p-1 }$条转录本集合${ \mathcal{T} }$,然后去寻找一条新的转录本${ T’ }$,寻找的方法是求解下面的规划${ P_1 }$
然后我们将${ T’ }$以及${ \sigma(T’) }$的所有子集代表的转录本,与${ \mathcal{T} }$合并,得到${ \mathcal{T}’ }$. 然后,用下面的数学规划${ P_2 }$重新估计丰度
然后我们得到${ \mathcal{T}’ }$的丰度估计${ c’ }$(此时${ c’ }$是向量),然后我们根据${ c’_i L’_i }$进行排序,保留top ${ p }$个转录本. 然后终止条件有下面两个,满足一个就可以终止,(1)${ p=k }$,即迭代到最大的数目;(2)${ \mathcal{T}’ = \mathcal{T} }$,即和上一步的结果保持已知(这个地方,我看了伪代码之后,也很困惑,因为每次${ p }$会增大${ 1 }$,思考之后我觉得有可能,再重新分配丰度的时候,有些转录本的丰度变成了${ 0 }$,所以就有可能前后两次迭代的结果一致.)
过滤假阳性的dicontinuous edges
JUMPER要求每个dicontinuous edges必须有100个read的支持,才会放入segment graph. 另外一个参数,文章测试发现丰度排名前${ 35 }$的dicontinuous edges足够抓住很多转录本. 更大的参数可以用来捕捉更复杂的转录本. 文章默认参数是${ 35 }$.
Results
首先给一个定义,如果一个discontinuous edges ${ v=[v^-,v^+],w=[w^-,w^+] }$是经典的,即${ v^+ }$落在转录调控先导序列(TRS-L)中,即位置${ 55-85 }$之间,且第一个‘AUG’出现在${ w^- }$的下游,且和已知的ORF的起始密码子重合。反之,称为非经典的。 一个转录本是经典的,当且仅当至多含有一条经典的边,以及没有非经典的边。(换言之,经典转录本要么从头到尾不跳跃,要么只在适当的位置跳跃一次)
Simulations
正确的标准,一个预测的转录本被认为是正确的,如果存在一个真实的转录本与之匹配,即junctions positions是匹配的(误差10个核苷酸之内). 由此可以计算出${ precision,recall }$,结果如下图Fig.4
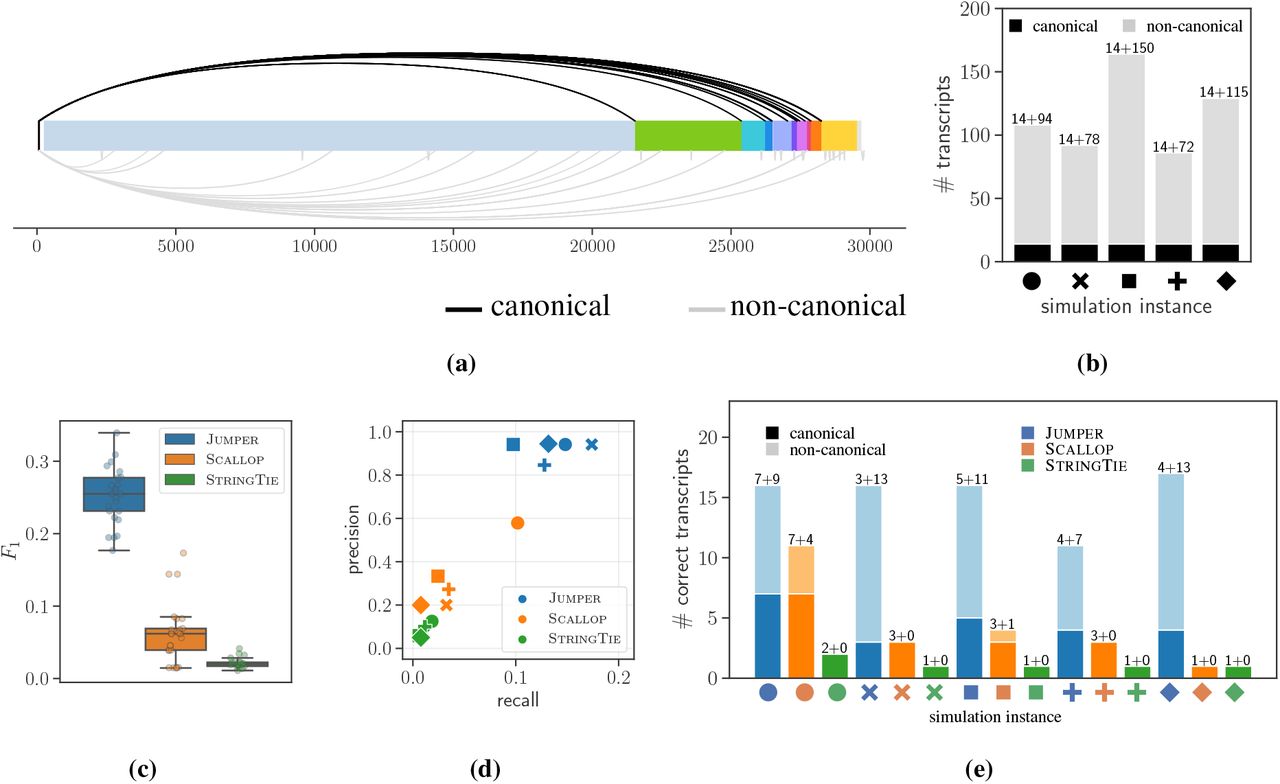
Fig.4 Simulated SARS-Cov-2 data1.
Transcript assembly in SARS-CoV-2
JUMPER组装了另一个数据集SARS-CoV-2,被二代、三代都测了一遍,用三代测序回贴发现了一些非经典的转录本,这些转录本同样被JUMPER用二代测序进行组装.如图Fig.5
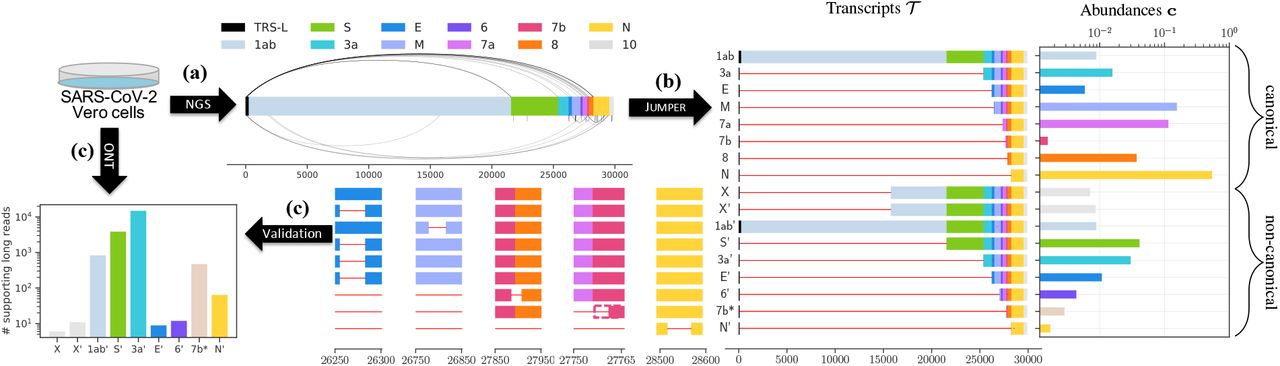
Fig.5 Assembly in SARS-CoV-21.
Appendix
Lemma 1. 令${ D>0 }$是一个常量,${ \overline{c}_ i (c) = c_i D / \sum_{j=1}^k c_j L_j}$,和${c_i (\overline{c}) = \overline{c}_ i / \sum_{j=1}^k \overline{c}_ j \ ,\forall i\in [k]}$. 那么${( \mathcal{T},c = [c_1(\overline{c}),\cdots,c_k(\overline{c})]) }$是上述数学规划(18)-(21)的最优解,当且仅当${ (\mathcal{T},\overline{c} = [\overline{c}_ 1(c),\cdots,\overline{c}_ k(c)]) }$是下面数学规划的最优解
Proof: 首先给出一个Claim
Claim-对于任意给定的标量${ \alpha>0 }$,我们可得
具体的推导不再赘述,仔细观察就能发现,${\log Pr(\mathcal{R} \mid \mathcal{T},\mathcal{c}) =\sum_{j=1}^m \left( d_j \log \sum_{i\in X(\mathcal{T},\sigma^{\oplus}_ j,\sigma^{\ominus}_ j)} c_i \right) -n \log \sum_{b=0}^{k} c_b L_b }$前面一项求和出来会多出${ n \log \alpha }$后面一项再减去${ n \log \alpha }$,所以是一样的. ${ \triangle }$
下面我们证明Lemma 1,记原始的(18)-(21)的最优化问题为${ P }$,新的(22)-(25)的规划问题为${ Q }$,(18)中的目标函数记为${ J(\mathcal{T},\mathcal{c}) }$,(22)中的目标函数为${ K(\mathcal{T},\overline{c}) }$
显然,
首先证明${ \Rightarrow }$,令${ (\mathcal{T},\mathcal{c}) }$是${ P }$的最优解,然后证明,${ (\mathcal{T},\overline{c}) }$是${ Q }$的最优解. 根据${ \overline{c} }$的定义,满足Q的约束((24)&(25)),所以${ (\mathcal{T},\overline{c}) }$是${ Q }$的可行解. 我们设${ (\mathcal{T’},\overline{c}’) }$是${ Q }$的最优解,则
令${ c’ = [c_1(\overline{c}’),\cdots,c_k(\overline{c}’)] }$,,因为${ c’ }$满足${ P }$问题的约束,所以${ (\mathcal{T}’,c’) }$是${ P }$问题的一个可行解,我们又知道${ (\mathcal{T},\mathcal{c}) }$是${ P }$问题的最优解. 故
我们观察到${ c’,\overline{c}’ }$仅仅相差一个系数${ \alpha = 1 / \sum_{i=1}^k \overline{c}’_ i }$,所以根据Cliam,${ J(\mathcal{T}’,c’) = J(\mathcal{T}’,\overline{c}’) }$;同理,${ J(\mathcal{T},\mathcal{c}) = J(\mathcal{T},\overline{c}) }$,然后式子(62)可以改写为
利用式子(61),以及${ Q }$问题的约束(24)可得
所以${ K(\mathcal{T},\overline{c}) = K(\mathcal{T}’,\overline{c}’) }$,${ (\mathcal{T},\overline{c}) }$是${ Q }$的最优解. 上述证明思路,可以再参照Fig.6
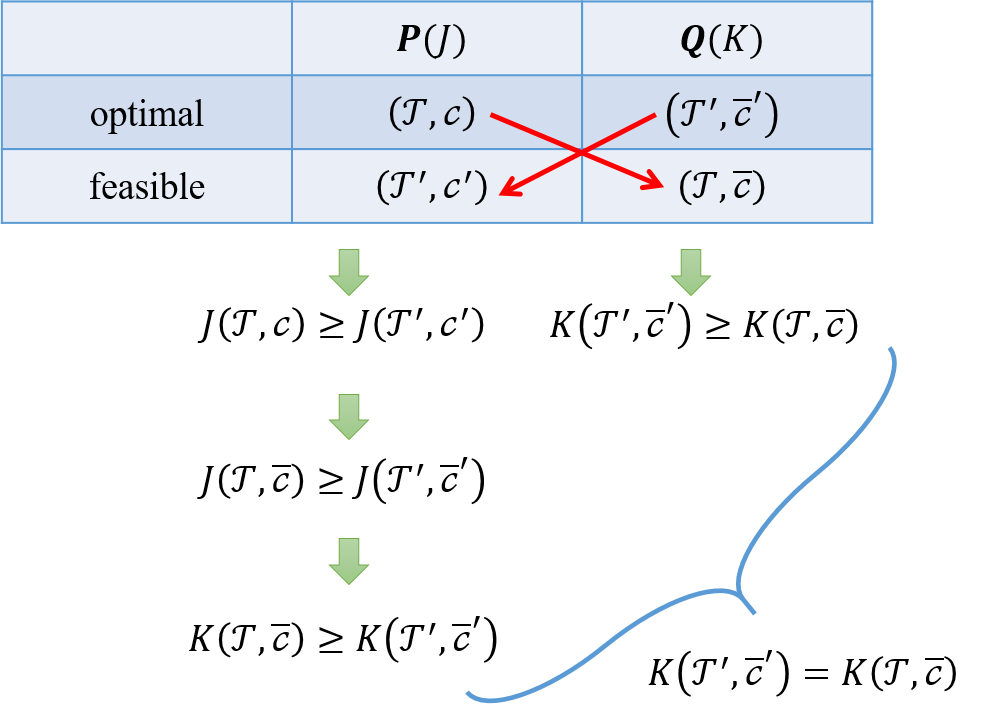
Fig.6 Clue of Lemma 1.
反过来${ \Leftarrow }$,同样的技巧可以证明,不再赘述. ${ \square }$