这篇博客向大家介绍三代基因组组装软件Flye，这是Pavel A. Pevzner在2019年发表在nature biotech上的工作. Flye通过构建repeat gragh来表示基因组，同时在解决repeat问题上提出了一个非常好的思路.

Introduction

关于repeat graph，大家可以参考这篇博客文献分享：De Novo Repeat Classification and Fragment Assembly，关于三代测序的基因组组装问题，大致有两种思路，一个是“correction then assembly”，一个是“assembly then correction”，Flye采用的策略是先拼接后矫正，我想原因在于不矫正read，保留read的原始信息，才有可能解决unbridged repeat. 具体的原因，请在Methods部分细细品味.

Methods

为了更细致的理解Flye的思想，以及保持一些术语的统一，再这里我仍然按照Flye的行文思路进行讲解，当然一些思路和结论我们在博客文献分享：De Novo Repeat Classification and Fragment Assembly已经提及. Flye在方法部分，仍然是先介绍repeat characterization problem，然后引出repeat graph来解决repeat characterization problem，最后再给出repeat graph和assembly之间的关系.

Repeat characterization problem

考虑有向图${G}$和图中的一个长度为${n}$的tour ${T=v_1,v_2\cdots,v_n}$，我们称${i}$th和${j}$th顶点是等同的，如果他们对应图中的相同顶点，即${v_i = v_j}$. 这些等同的点${(i,j)}$，我们可以将其绘制在一个二维的网格中，我们称这个网格图为tour ${T}$的repeat plot ${Plot_T (G)}$. 如果已知${G,T}$，得到repeat plot ${Plot_T (G)}$是一个非常容易的问题.

而我们更关注这个问题的反问题，任给一个${Plot}$，来寻找图${G=G(Plot)}$和tour ${T}$.

基因组的dot-plot其实是一个矩阵，可以图表化genome中的所有repeat. 在repeat characterization问题中，我们关注于genome自身的local-alignment，那么每个一self-alignment对应基因组两个连续的repeat片段（segment）${x,y}$，${x}$和${y}$称为该alignment的${spans}$. 给定一个长度为${n}$的genome，以及自身比对的${Plot}$，Repeat characterization problem等价于构建图${G}$以及长度为${n}$的tour ${T}$（基因组的每个segment对应tour ${T}$中的subpath），其中${Plot=Plot(G)}$，tour ${T}$是符合alignment结果的.

Generating repeat plot of genome

Flye生成基因组的所有self-alignments，然后组合成repeat plot ${Plot}$.

Constructing a punctilious repeat graph

令 Alignment = Alignment(Genome,minOverlap)，是基因组’Genome’中充分长的self-alignment的集合（长度最少是’minOverlap’）. Flye设置’minOverlap’为read-set的N90（在这篇文章的数据集中，N90大致是${3000-5000bp}$）

给定了’Genome’的self-alignment的集合’Alignment’之后，接下来我们构建punctilious repeat graph，即一丝不苟的repeat graph RepeatGraph(Genome,Alignment). 得到的方法就是将’Alignment’比对上的positions ‘gluing’到一起. 然后将分支顶点之间的simple path收缩为一条边，这条边的长度等于原始path的边的数量. 这个图就是punctilious repeat graph，我们按照阈值${d=500}$，将边分为long和short.

之所以这样做，是为了下面简化punctilious repeat graph做铺垫，punctilious repeat graph在真实的基因组中会非常复杂，’gluing’操作会产生许多branching point.

From punctilious repeat graph to repeat graph

在比对的时候，repeat的端点很难完全对齐，那么在’gluing’之后，就会产生复杂的结构，比如分支顶点和short edge（${<d=500}$）. repeat graph RepeatGraph(Genome,Alignment,${ d }$)定义为将punctilious repeat graph的short read收缩之后的图. 具体的收缩操作，就是将边的endpoint进行’gluing’，然后移除loop-edge. 考虑基因组tour，穿过repeat graph多次的就是repeat edges，一次的称为unique edge.

Approximate repeat graphs

在FragmentGluer中，花了很多的经历来处理Whirl/Bullbe，但是在三代测序中这些处理的很多参数很难抉择，因此我们采用下面的方法进行处理，只关注于self-alignment的端点.

考虑punctilious repeat graph中导致repeat graph中的branching vertices的顶点集合${V}$，令Breakpoints=Breakpoints(Genome,Alignment,${d}$)，是导致${V}$的基因组的位置集合. 在Fig.1中，${V={A,B,D,E}}$，Breakpoints=${{1, 2, 4, 5, 7, 8, 9, 10,12, 13}}$.

Fig.1 Workflow of constructing repeat graph¹.

Flye选取’Alignment’中的endpoints在主对角线上的投影点来近似Breakpoints集合. 两个endpoint被称为close，如果他们在主对角线上的两个投影有一对是小于阈值${d}$的（允许一个水平投影，一个竖直投影）.然后，Flye将endpoints按照close的关系，进行聚类. 聚成一类的endpoints被’gluing’到一起，进一步将平行边进行合并. Fig.2中（${d=0}$）作为示例，展示了Approximate repeat graphs的构建过程，同一个颜色的点就是被聚到一类的endpoints.

Fig.2 Workflow of constructing Approximate repeat graphs¹.

Extending the set of breakpoints

之前我们提及过inconsistent alignment，理论上，${m}$个重复片段应该形成${\tbinom{m}{2}}$个比对，但是由于各种原因，${m}$个重复片段有一些两两比对没有被捕获，这就产生了inconsistent alignment. 那么这将导致一些’Breakpoint’的缺失. 比如Fig.3所示，由于缺失了${B_2,B_3}$之间的比对，所以紫色的方块位置的点没有归入’Breakpoints’集合. 因此就没有鉴定出来其中${A_2+B_2}$的镶嵌结构.

所以要进行’Breakpoints’集合的扩充，一个alignment-path中的点称为合法的，如果其两个投影点（水平、竖直）都属于’Breakpoints’集合，如果仅有一个，则称为非法的. 如果’Breakpoints’集合全部是合法点就称为合法的，否则称为非法的. Flye通过迭代的方法，试图加入最少的positions，使得’Breakpoints’集合成为合法的. 具体操作是为非法点加入missing的投影点，直到’Breakpoints’没有非法点.如Fig.3所示，因为五角星点只有一个投影点属于’Breakpoints’，为非法点所以加入方块点后，’Breakpoints’集合成为合法的.

Fig.3 Extending the set of breakpoints¹.

然后，和上面描述的一致，对’Breakpoints’集合中close的顶点进行合并，那么聚类的时候，其实在主对角线上，形成了segments（也就是cluster里面，位置最小和最大的之间的区域），因此这个新的集合称为’BreakpointSegments’，里面的元素称为segment. 两个segment是等价的，如果存在一个alignment-path的一个点，其两个投影分别落入两个segment中，如图Fig.4所示. 所以，通过这样，我们将segment进行聚类，那么合并Segment的时候，Flye选择只’gluing’ segment的middle points.

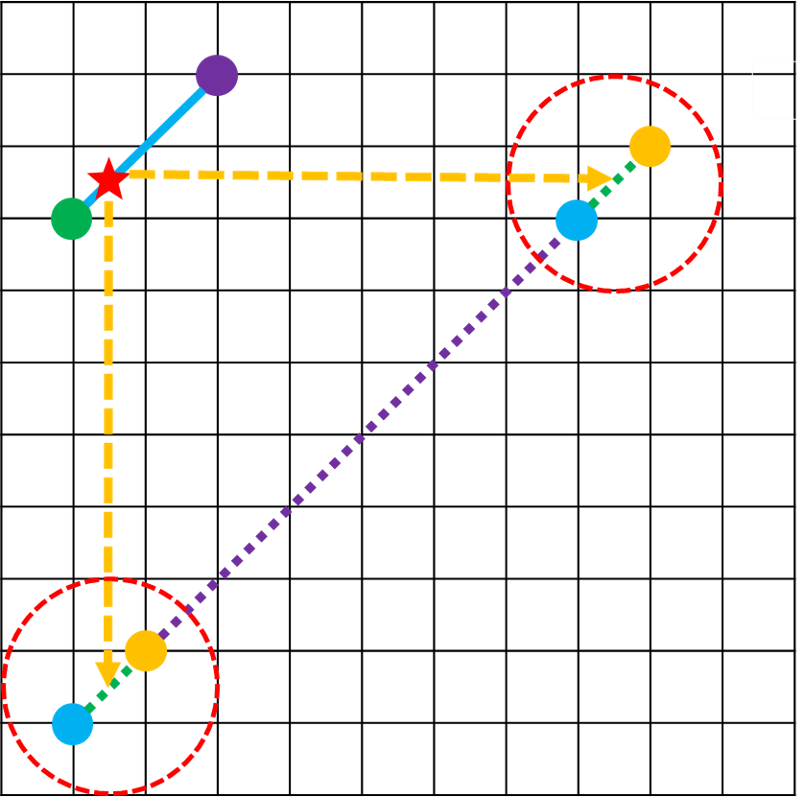
Fig.4 Equivalent segment.

Phased summary

我们简单梳理一下前面的思路，我们理论上需要从Genome，得到Alignment，然后构出punctilious repeat graph，再进一步得到repeat graph. 但是这样得到的repeat graph还需要进行复杂的去除Whirls/Bubbles的过程，因此我们选择只合并close的’Breakpoint’得到Approximate repeat graph，实际的操作上，我们使用’endpoints’的投影和’Extending breakpoints’操作得到’BreakpointSegments’，通过合并segment的middle points，再进一步如果平行边在’Alignment’中被比对，则进行合并来实现对于repeat graph的近似. 在后面的讨论中，我们简称Approximate repeat graph为repeat graph(RG).

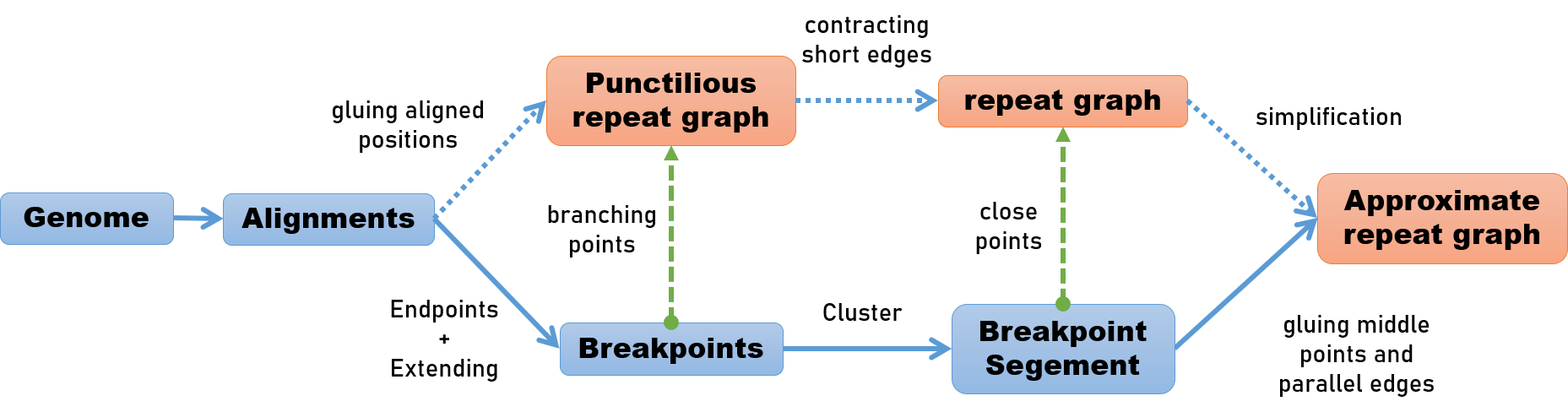
Fig.5 Phased summary.

Genome assembly

常见的拼接思路是，首先基于read构建assembly graph，再利用一些操作或者信息（例如piared-read）来解决repeat问题，最后输出contig. Flye认为更好的方法是继续基于contig构建assembly graph（这样的图会更简洁），然后进一步在这个图中去解决repeat问题. 这种思路的另一个好处是，容易结合一些二代三代数据混合拼接的思路.

ABruijn assembler构建contigs的方法，就是不断的延伸read，直到出现不能决定的地方（branching vetex in (unkonwn) repeat graph）. read延伸的时候，需要至少‘minoverlap’的重叠.

Constructing disjointigs

令${UnprocessedReads=AllReads}$，从中任选一个read，然后进行延伸（保证至少‘minoverlap’的重叠），直到无法延伸，生成${ChainOfReads}$. 然后将${AllReads}$中的reads，全长比对到这个序列上，这一部分reads将被${UnprocessedReads}$集合中删除（这样可以加速disjointgs的构建过程）. 然后，再用minimap2将read比对到${ChainOfReads}$上进行纠错，得到${ DisjiontigSequence }$. 这个过程，附录中说，可以将disjointig序列的错误率从${13\%}$提高到${1-5\%}$.

在延伸reads时候，其实Flye采用了并行的策略，所有${UnprocessedReads}$集合中的read都同时进行延伸，如果一个线程完成了，就和之前的disjointigs比对，如果和一个之前的disjointig重叠超过${10\%}$，就将这个disjointig删去，同时read释放回${UnprocessedReads}$集合.

Constructing assembly graph from disjointigs

然后将disjointigs按照任意顺序连接（用分割符隔开），得到序列${Concatenate}$，然后进行进一步得到’${Alignment}$’，按照Repeat characterization problem的描述，最终得到RepeatGraph(Concatenate,Alignments,${d}$). 这个RepeatGraph和基因组得到的repeat Graph是一致的，在博客文献分享：De Novo Repeat Classification and Fragment Assembly已经说明.

Resolving bridged repeats

Flye将reads比对回assembly graph，这里需要注意，对于每个repeat edge，Flye储存了多个拷贝（序列来自于原本的disjointigs）. 所以Flye将read和所有这些拷贝都进行比对，选择一个最好的比对进行保留.

进一步，Flye首先计算整个grpah的平均测序深度${cov}$，然后将edge分为${low-coverage}$（深度小于${2\times cov}$），和${high-coverage}$（深度至少为${2\times cov}$）. 然后再重新精确分类，刚才read比对回图上之后，我们可以得到read-path（read支持的path），一个边${e’}$被称为${e}$的successor，如果存在一个read-path${e’}$在${e}$的后面，对于${low-coverage}$且仅有一个succesor的边，被分类为unique，其余的边被分类为repetitive.

因为下面要介绍Flye怎么解repeat，所以这里先介绍一下bridged repeats和unbridged repeats（见图Fig.6），所谓bridged repeats就是指，存在一个read，能够跨过repeat区域，这样的话，我们在面对repeat区域的时候，就可以判定如何通过；如果不存在，就是unbridged repeats，那么处理起来就非常麻烦，有可能无法解开这个repeat.

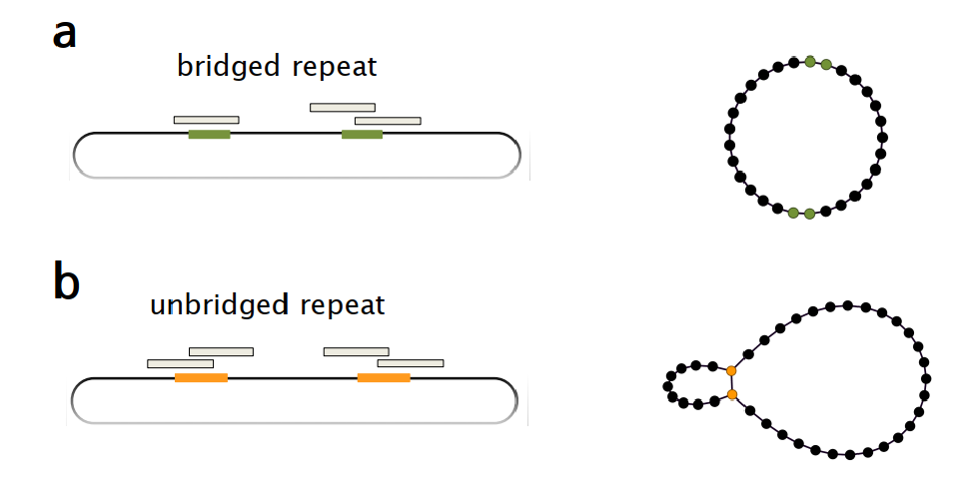
Fig.6 Bridged repeats and unbriged repeats².

Untangling incident edges ${ e = (w, v) }$ and ${ f = (v, u) }$ in the condensed assembly graph amounts to substituting them by a single edge ${ (w, u) }$. 我觉得这一步的意思，是按照Fig.7进行操作.

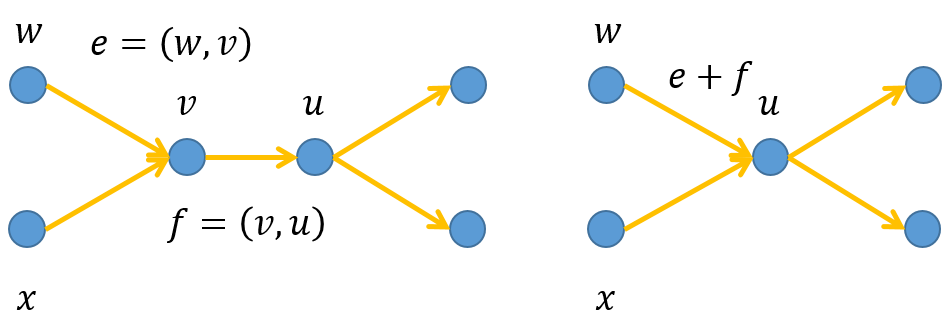
Fig.7 Condensed assembly graph.

因此，bridging read在condensed assembly graph被称为${(e,f)}$-read，如果其穿过两条连续的边${e,f}$的话. 我们在condensed assembly graph中定义一对偶联的边${e,f}$的‘transition${( e,f )}$’，其值为${(e,f)}$-read和${(f’.e’)}$-read之和（${e’,f’}$指的是${e,f}$的反向互补序列对应的边）.

然后构建transiton graph，condensed assembly graph中的每个边${e}$，都对应两个顶点${e^h,e^t}$，也就是${e}$的head和tail顶点. 每个${(e,f)}$-read对应transition graph的一个无向边${{e^t,f^h}}$，权重等于transition(e,f). 在transition graph中，Flye调用最大权匹配算法，寻找到最大匹配之后，对于每个匹配${e^h,f^t}$，计算与${e^h}$或者${f^t}$邻接的边的总权重${TotalWeight}$，如果transition${(e^h,f^t)<TotalWeight/2}$，那么这个边将被忽略，因为支持这个路的read太少了. 最后Flye就这样迭代的解开一些边，再接着寻找最大权匹配，直到没有bridged能解的repeat.

Resolving unbridged repeats

Flye解决unbridged repeat的思路是利用不同的repeat区域之间，一般不会完全一致，会出现微小的变异（当然这里，其实还有个重要的条件，就是对于二倍体的生物，其repeat之间的差异大于两个同源染色体的差异，在文章的附录中，给出了具体的数据，repeat之间的差异在~${4\%}$，而同源染色体的SNVs大约是${0.1\%}$）. Flye目前只能解决单倍体或者二倍体的二次重复的情况，换句话说，repeat的重复次数大于2，Flye是无法解决的.

具体地，Flye首先将read比对到REP edge的两侧，因此我们可以向前移动，分别构建一致性序列，这样就将repeat的区域缩短，迭代的进行，直到出现bridging read.

Fig.8 Resolving unbridged repeat¹.