我们知道基因组拼接中,一个难点就是在Assemble graph中repeats区域的路径选择问题.当然了,这个问题的解决是非常复杂的.这篇文章其实非常早了,是2004年非常著名的Pavel(这个人全名叫Pavel A. Pevzner,在重新整理这篇文章的时候我发现GR网站上里面名字居然是Paul A. Pevzner,而在Pubmed上是我们熟悉的名字,可能是因为这个人是俄罗斯人,后来自己更换了英文对应的音译)发表在Genome Research上的文章.
为什么分享这篇古老的文章呢,因为这篇文章是19年发表的Flye中repeat graph的思想来源,能够解释Flye里面很多处理方法的原理.简单说一下这篇文章的内容,这篇文章分为两个部分,第一个部分是解决了所谓的repeat representation问题(repeat classification),第二部分,借由上面的思想提出了一个组装基因组的方法FragmentGluer.
Introduction
我们先来介绍一下repeat的结构,可能我们认为repeat不就是基因组上重复出现的片段嘛,这有什么结构呢?其实不然,在这篇文章中,repeat其实代表了一个区域,这个区域由许多sub-repeats构成,也就是呈现所谓的镶嵌结构.我们来看一个真实的例子,Fig.1是人类Y染色体上repeat区域的一个示意图,虚线表示没有重复的区域,彩色的表示重复区域,同一种颜色表示一种sub-repeat,可以看到图中的三个repeat区域是不同的sub-repeat排列组合而成.
Fig.1 Mosaic repeat of human Chromosome Y1.
那么为什么会形成这样的结构呢,Fig.2是一个想象的基因组进化的过程图,因为每次repeat片段的转移,都是因为染色体结构变异,然而结构变异恰好每次都一样的概率是很低的,所以会出现sub-repeat的结构.
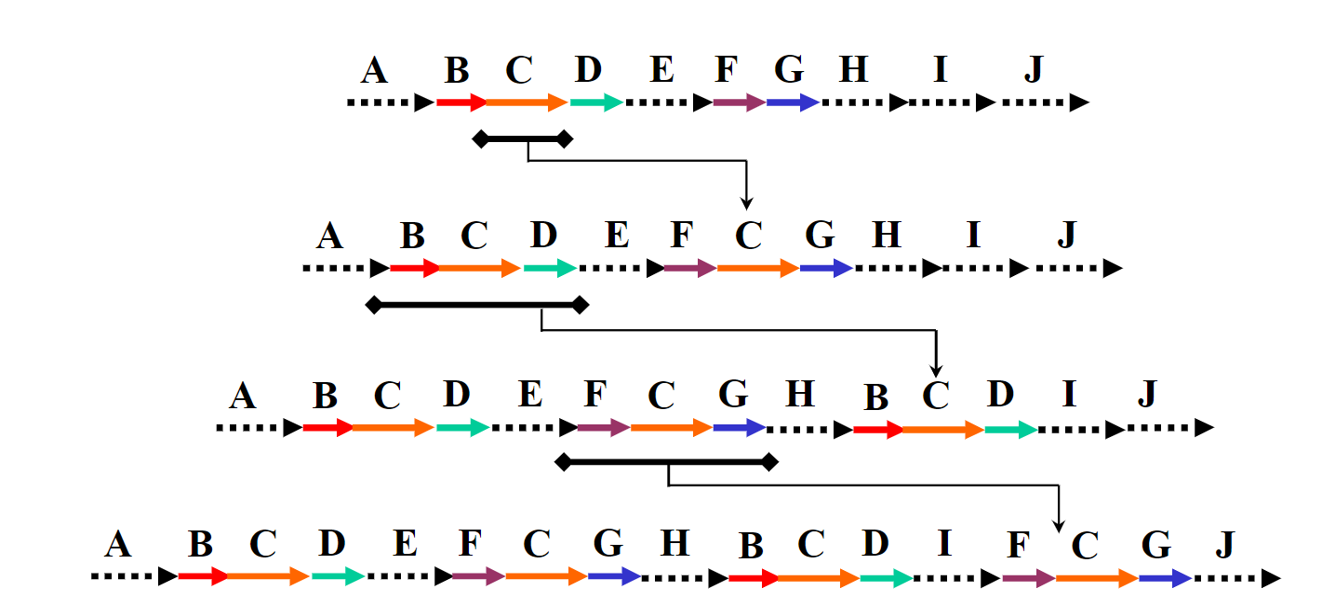
Fig.2 Repeats’ evolution1.
所以我们的任务来了,所谓的repeat classification problem或者repeat representation问题指的就是将上面这些sub-repeat的边界界定出来,严格来讲,我们最重要构造出来所谓的repeat graph,如图Fig.3
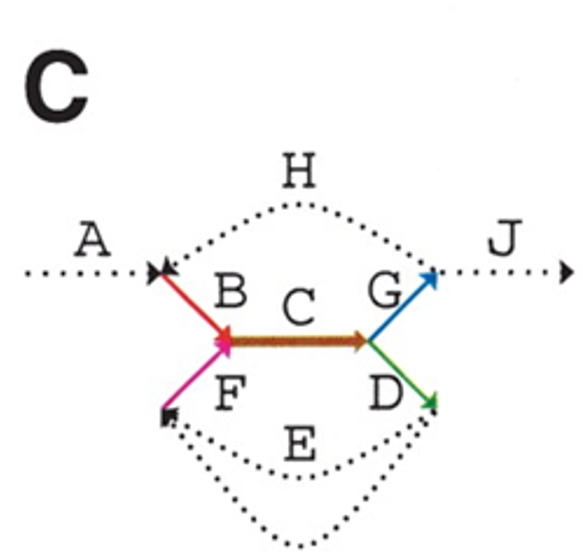
Fig.3 Repeat graph1.
Methods
${A}$-Bruijn Graphs
首先我们引入Genomic dot-plot的概念,我们将基因组自身进行local alignment,在比对上的坐标位置绘制一个点,我们可以得到所谓的dot-plot,如图Fig.4
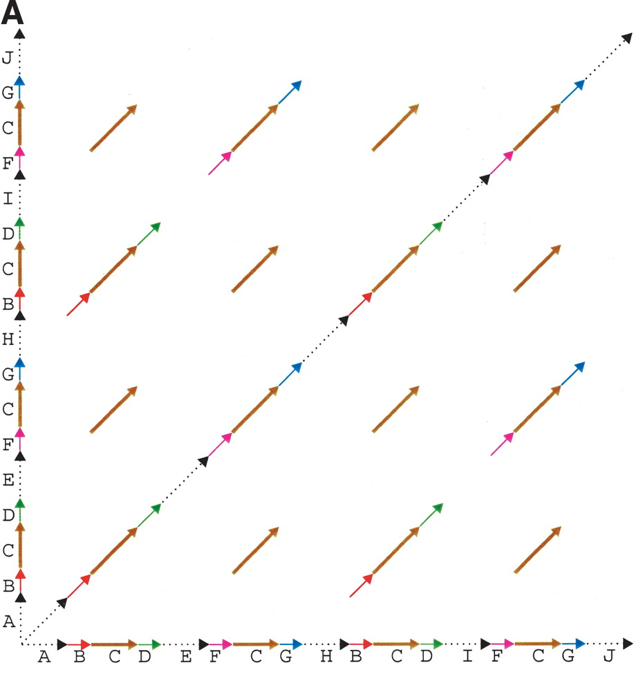
Fig.4 Genomic dot-plot of an imaginary sequence1.
令${S}$是一个长度为${n}$的基因组序列,同时${A=(a_{ij})}$是一个${0-1}$的二元${n\times n}$的“similarity matrix”表示${S}$中的区域之间显著的local pairwise alignment的集合${\mathscr{A}}$.矩阵${A}$中,如果位置${i}$和位置${j}$比对上,则${a_{ij}=1}$,否则为${0}$(插入缺失不记录在${A}$中).
我们可以将矩阵${A}$视为一个邻接矩阵,这个邻接矩阵对应了一个图,我们称为${A}$-graph,这个图有${n}$个顶点,顶点${i}$和顶点${j}$存在边,当且仅当${a_{ij}=1}$.令${V}$是${A}$-graph的连通分支集合,${v_i\in V}$表示包含顶点${i}$的连通分支(容易想象,每个连通分支中的点就是相互比对上的顶点).
下面我们来定义多重图(multigraph)${A}$-Bruijn graph ${G(V,E)}$,其中${V}$中的每个顶点就是${A}$-graph的连通分支,连接${v_i,v_{(i+1)}}$.(换言之,在${A}$-Bruijn graph中,按照基因组本来的顺序连接这些顶点,即${A}$-graph的连通分支),其中${v_1}$称为source,${v_n}$称为sink. 换个角度,可以认为我们将从${1,\cdots n}$的欧拉路按照比对的关系,收缩为一个点。
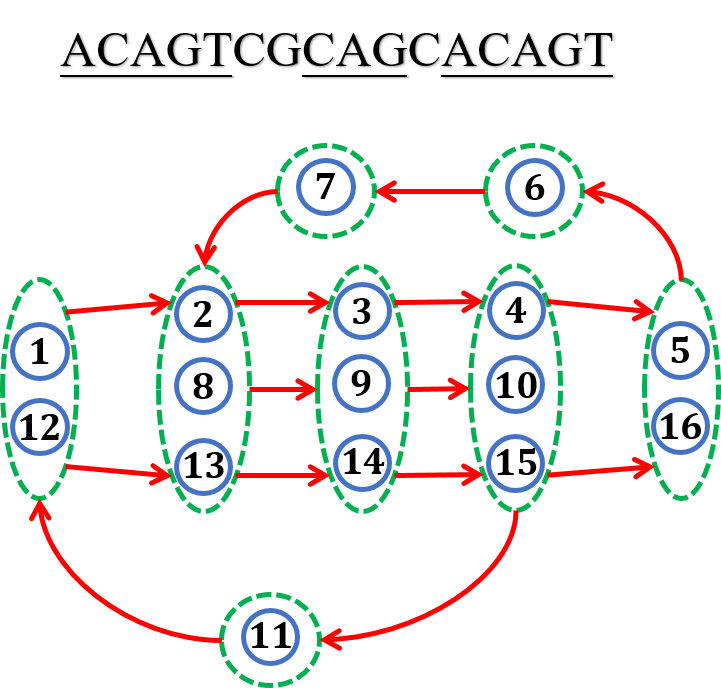
Fig.5 Eaxmple of ${A}$-Bruijn graph.
Cleaning Up Whirls and Bulges
What and Why
${A}$-Bruijn graph我们也可以将多重边视为权重。我们给定一个阈值${girth}$,那么所有长度短于${girth}$的圈视为short cycle。那么圈分为两类,①Whirls指的是全中所有边方向相同的短圈;②Bugles表示圈中存在反向边的短圈,如图Fig.6所示
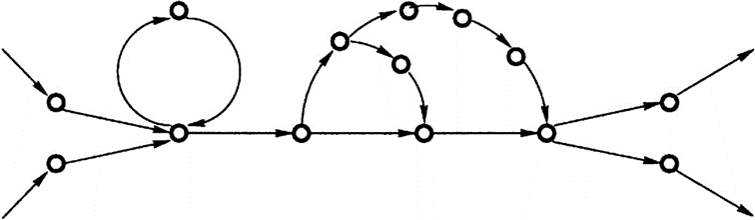
Fig.6 Whirls and Bulges1.
下面我们讨论一下二者的成因,Whirls是由于“inconsistent alignments”造成的,那么什么是inconsistent alignments呢?我们可以通过Fig.6来理解一下,由于比对的问题,我们将${–at}$比对到了${acat}$上,而这就导致了这三个序列的第一个${a}$比对错位的状态。(个人理解:理论上,在${A}$-graph的每个联通分支内部应该是一个完全子图),所以因为不一致的比对,我们将第二个${a}$也收缩进了一个${a}$的联通分支,所以出现了循环的Whirls的结构。在Fig.6B中为${a\rightarrow c \rightarrow a}$。当然,Whirls另一个成因是因为短串联重复序列(short tandem repeats),比如${\textbf{ATTCGATTCGATTCG}}$,这里${\textbf{ATTCG}}$重复了三次,在这篇文章,作者假设短串联重复序列在比对集合${\mathscr{A}}$中不存在。而Bugles是因为alignment中的gap导致的,比如${ac-t}$和${acat}$的比对,产生了两条path,形成了Bugle,分别为${c \rightarrow t}$以及${c \rightarrow a \rightarrow t}$.
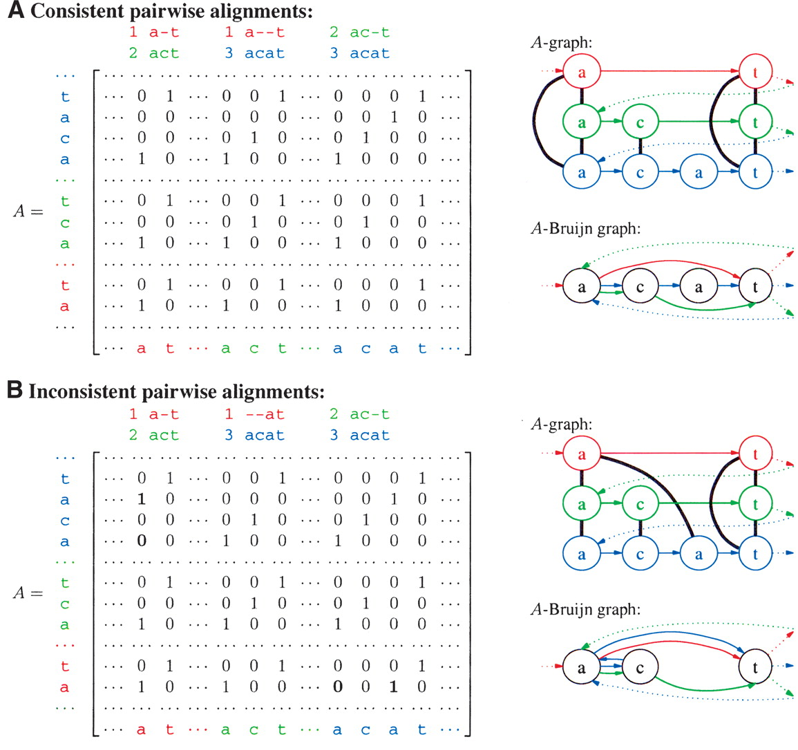
Fig.7 Consistent pairwise alignments and inconsistent pairwise alignments1.
Cleaning Whirls
对于${A}$-Bruijn graph中的顶点${v}$,令${P(v)}$表示其对应的${A}$-graph中的联通分支的顶点集合(基因组位置集合)。我们定义顶点${v}$是“composite”,如果${P(v)}$包含两个距离在${girth}$之内的基因组位点。这些位点就是潜在的“inconsistent alignments”所在的位点. 这部分的处理思想呢,就是将composite的顶点分成两个点。
算法采用迭代的方式进行,每次寻找${A}$-Bruijn graph中,连接composite和noncomposite顶点的所有边中权重最大的称为“split edge”,设边的权重(重边数)为${m}$,${v}$是这条边邻接的composite的顶点,那么这条边的权重为${m}$对应着${P(v)}$中${m}$个位点和后继位点的连边,我们将${P(v)}$中这${m}$个点的集合记为${M}$,(注意到${m<\lvert P(v)\rvert}$,设split edge邻接的noncomposite顶点为${n}$,因为如果${m=\lvert P(v)\rvert}$,那么意味着${P(v)}$后继位都包含在${P(n)}$中,那么${n}$是一个composite顶点,矛盾!)
所以我们可以将顶点${v}$分成两个顶点,分别为${P(v) \setminus M}$和${M}$收缩为的顶点. 然后将矩阵${A}$的相应元素的值进行更改,即${a_{ij}=0,\forall i\in M ,j\in P(v) \setminus M}$. 因为顶点${n}$是noncomposite顶点,所以拆分出来的${M}$对应的顶点一定是noncomposite. 这样每次我们至少产生了一个noncomposite顶点. 算法迭代进行,直到全部顶点变为composite顶点.(个人理解之所以每次选择边权重最大的,应该是可以减少迭代的次数,因为如此,我们每次尽可能多的拿走了${P(v)}$中的点),Fig.8是一个示意图
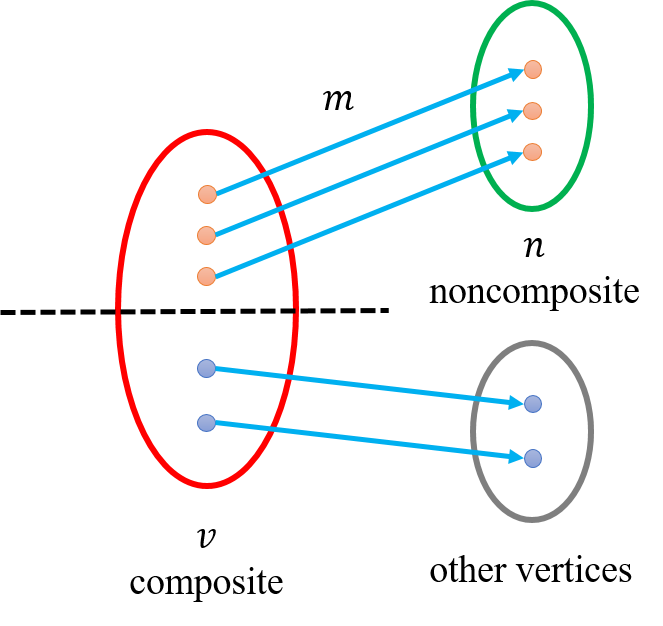
Fig.8 Processing of cleaning whirls.
Cleaning Bugles
Bugles往往在真实的情况下呈现网络的结构,如Fig.6所示,同时我们认为边的权重越大,说明这个边在repeat中越保守,所以我们想破除Bugles,同时保留权重大的边(换言之,因为repeat中间有gap才出现Bugles,两种走法,我们要进行统一,所以我们选择权重大的,也就是支持最多的走法为代表). 所以这里引入Maximum Subgraph with Large Girth (MSLG) Problem,MSLG问题想去寻找一个不包含Short Cycle(长度小于${girth}$)的最大权子图,如果${girth=\infty}$,这就是一个最大支撑树的问题,但是对于${girth \ne \infty}$,这个问题非常复杂,所以我们选择一个近似算法。
首先寻找最大支撑树${T}$,然后将剩余边按照权重从大到小排序,以次加入${T}$中,如果产生short cycle则抛弃,否则保留。
Erosion
再破除Bugles后,其实我们只是不再存在短圈,但是原本的Bugles还会剩余树状的末端,所以我们迭代的去除图中的叶子,也就是${degree=1}$的点(除了sink和source点外),直到图中只有sink和source点是度为${ 1 }$的点. 上述步骤的示意图见Fig.9
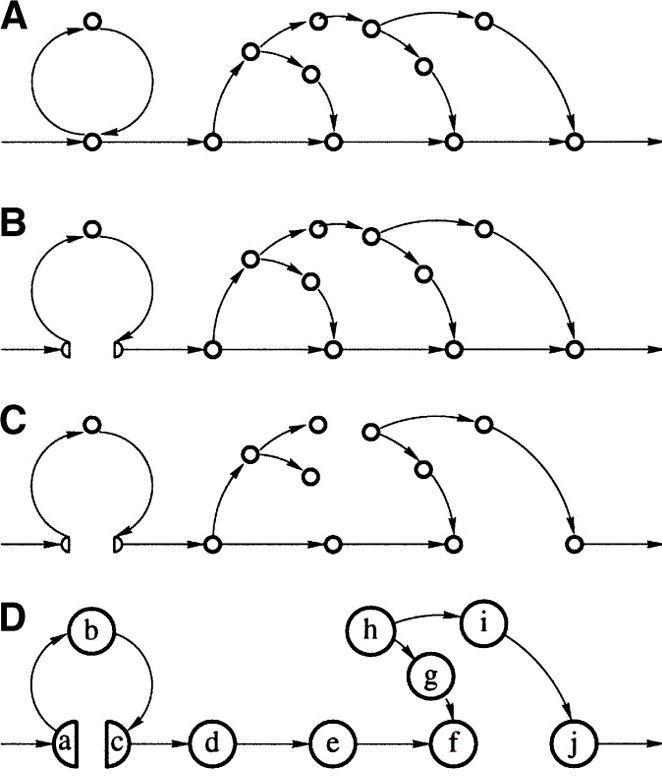
Fig.9 Cleaning up Whirls and Bulges and Erosion1.
Zigzag path and Consensus Sequence of Sub-repeats
经过Erosion之后,我们的图已经相当简单了,下面我们来得到consensus序列,其实很简单,每个顶点${v}$对应了相应的位置集合${P(v)}$,然后选择一个频率最高的碱基作为代表。
但是,在Fig.9中,我们发现,有一些path包含了foward和reverse边,这种就称为zigzag path,我们现在要将zigzag path拉直,从起点${s}$开始,到终点${t}$结束,每个内点${v}$,都会被我们计算从${s}$到${v}$之间正向边和反向边的差值,即${index(v)}$. 以Fig.8D为例,${a=s}$,其余点的${index}$值以次为,${\mathop{1}\limits_{b},\mathop{2}\limits_{c},\mathop{3}\limits_{d},\mathop{4}\limits_{e},\mathop{5}\limits_{f},\mathop{4}\limits_{g},\mathop{3}\limits_{h},\mathop{4}\limits_{i},\mathop{5}\limits_{j}}$,然后将相同${index}$的顶点合并,并将相应的${P(v)}$也合并. Fig.6的合并结果见图Fig.10
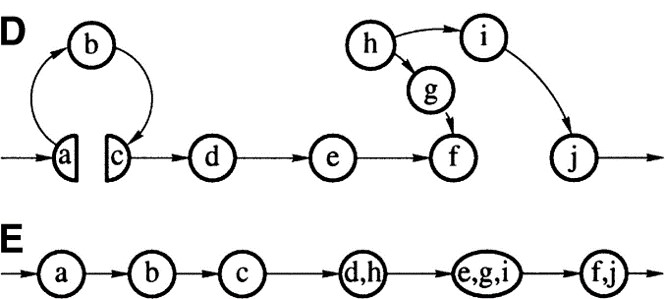
Fig.10 Zigzag path straightening1.
Threading the Genomic Sequence Through the Graph
因为前面的处理操作删除了很多顶点,所以${A}$-Bruijn graph的Eulerian path被打断了,我们现在的目标是的将片段连起来.
我们现在将${A}$-Bruijn graph ${G}$中的每个顶点${v}$都对应了基因组的位置${P(v)}$,我们将${P(v)}$中的位置用顶点${v}$进行编号,由于我们缺失了一些顶点,所以并不是所有的基因序列被我们编号. 将及基因组位置的顶点编号按照顺序排序,不妨设为${v_1,\cdots ,v_k}$,然后我们寻找${v_i}$和${v_{i+1}(1\leq i <k)}$之间的最长(顶点数目最多)的最短(权重最小)路,那么这些路合并起来,我们就可以认为将“删减”后的基因组走了一遍,这个过程称为“threading”. 这个过程结束后,我们得到了基因序列${S}$的consensus序列,也就是说,这个序列中所有的sub-repeats都被替换为了consensus序列,进一步我们可以将simple path合并为一条边,这样的图就被称为“repeat graph”在threading的过程中,可以根据边被${S}$的consensus序列穿过的次数来定义重数multiplicity,大于1的就是sub-repeat. 由此我们得到了repeat classification问题的结果,我们厘定了这些sub-repeat之间的连接关系. Fig.11展示了Fig.5的例子得到的最终结果
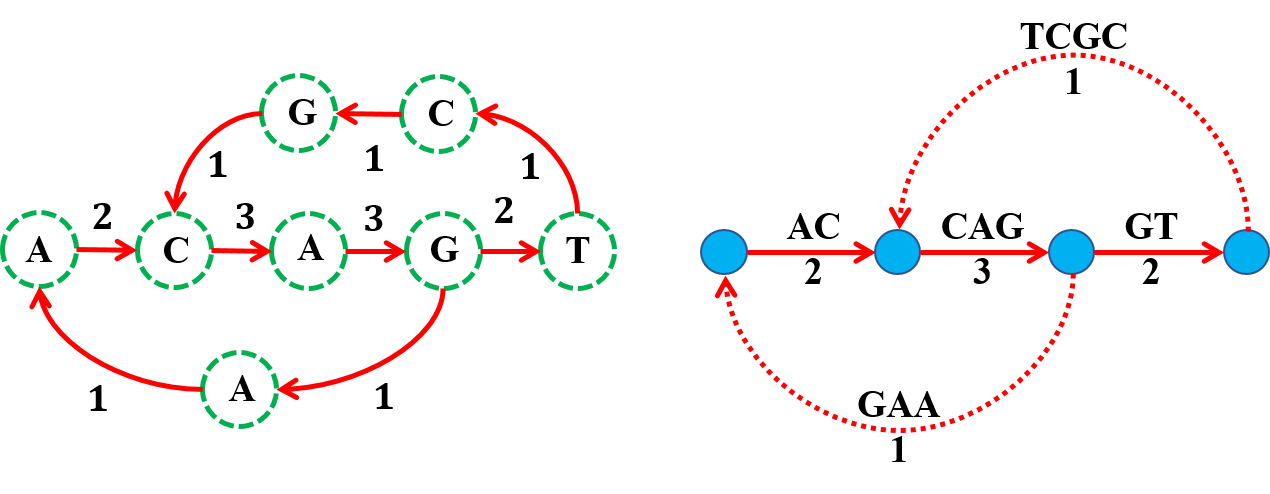
Fig.11 The resulting graph of sample.
Constructing ${A}$-Bruijn Graph Without the Similarity Matrix
这一部分是从repeat classification问题到Genome Assembly问题的关键.
在通常的情况下,我们是不知道基因组的全部序列的,那么我们是否还能解决repeat classification问题呢?我们很容易想到测序技术可以提供帮助. 设substrings集合${S_1,\cdots, S_t}$是基因组序列${S}$的一个“covering set”,也就是${S}$的每对连续的位置,都可以在${S_1,\cdots, S_t}$中的某个元素${S_i}$找到. 如果我们让${S_1,\cdots, S_t}$相互进行序列比对,那么实际上我们可以得到${S}$与自身进行local alignment得到的Similarity Matrix ${A}$的一个子矩阵(Fig.12),因为${S_1,\cdots, S_t}$覆盖${S}$,所以理论上我们可以推理出未知的矩阵${A}$.
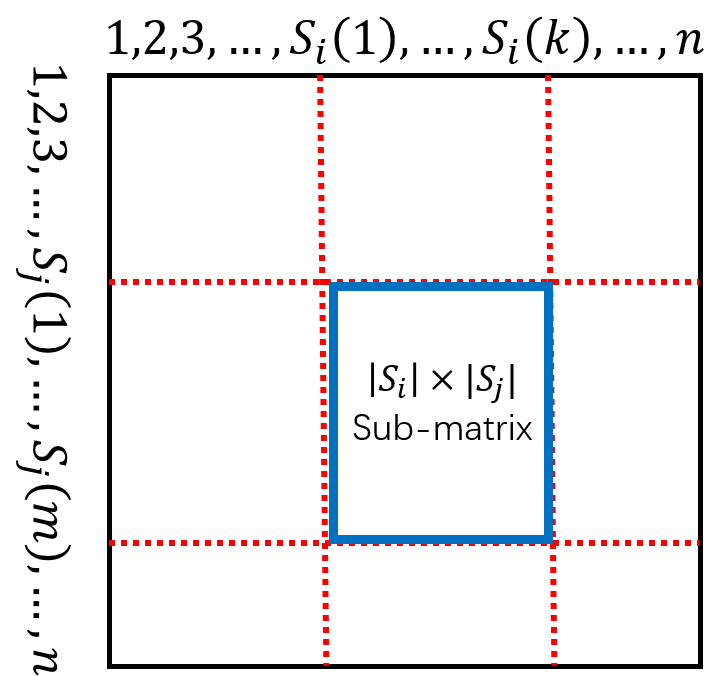
Fig.12 The snapshot of Similarity Matrix ${A}$.
现在的我们不知道${S_1,\cdots S_t}$在${S}$中的位置,但是我们可以证明,${S_1,\cdots S_t}$任意连接(序列的直接连接,而非通过overlap的组装)得到的序列${S’}$,及其相应的Similarity Matrix ${A’}$,所生成的${A’}$-Bruijn graph和${S}$生成的${A’}$-Bruijn graph是完全一致的. 道理也很简单,对于node ${i}$在substrings中的任何复制,都最后被捏在一起了,因为${S_1,\cdots S_t}$的覆盖,${S}$的所有边,都被${S’}$保存了至少一次. Fig.13展示了Fig.5的例子,如果通过测序read如何得到${A}$-Bruijn graph
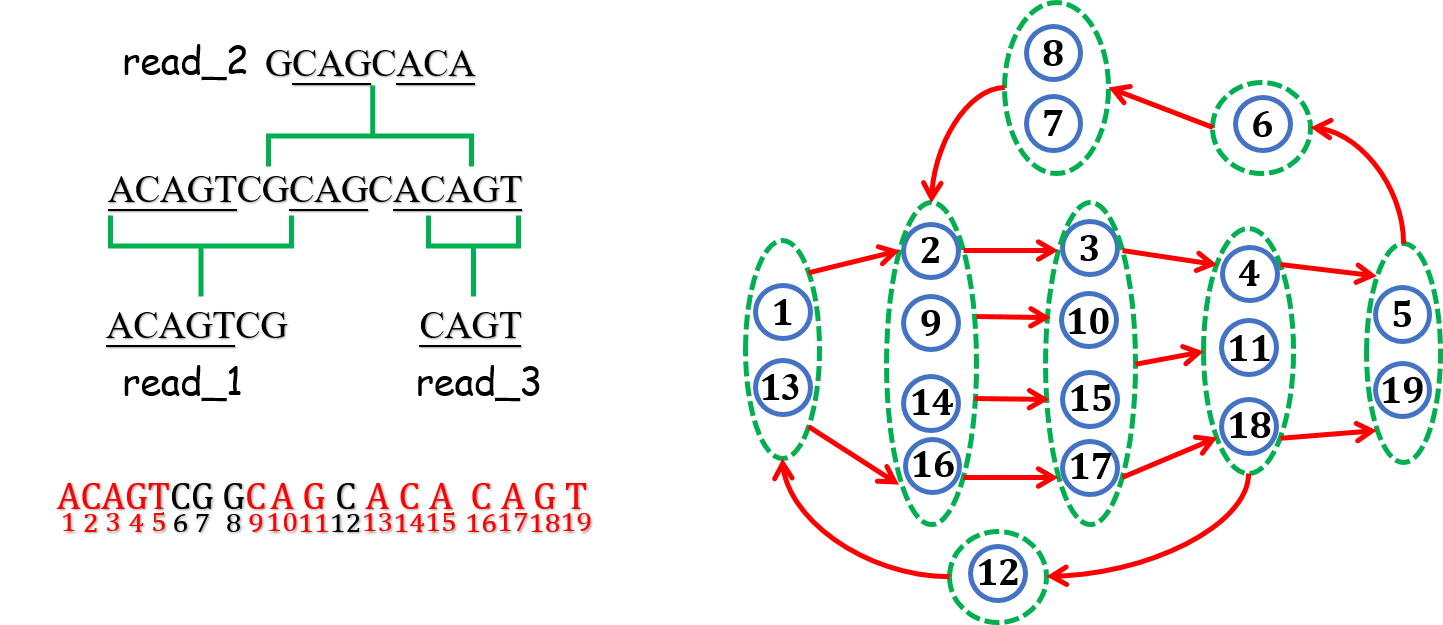
Fig.13 Constructing ${A}$-Bruijn Graph Without the Similarity Matrix.
Fragment Assembly
所以我们通过上面的方法,可以通过测序read得到repeat graph.具体步骤如下
0a.从${{S_1,\cdots ,S_t}}$中鉴别和移除嵌合体read(两个不相邻的基因片段,连在一起).
0b.任意连接read序列及其反向序列连接成一个序列,然后reads之间两两进行序列比对,得到Similarity Matrix${A}$.
1.构建矩阵${A}$的${A}$-Bruijn graph.
2.去除Whirls.(Mentioned before)
3.去除Bugles.(Mentioned before)
4.Erosion步骤,迭代${girth}$次去除叶子.
4a.为最长的path恢复步骤4去除的顶点. PS:因为现在我们并不知道souce和sink点是哪一个,因此我们选择迭代去除${girth}$次图中的叶子,并在4a步恢复,试图保护souce和sink点.
5.延展zigzag path.(Mentioned before)
6.按照read的序列顺序来thread graph,将read穿过顶点的次数定义为这个顶点的coverage(覆盖度),一个simple path的覆盖度指的是顶点覆盖度的平均值.
7.将simple path收缩为一条边,置于边的mutiplicity,这里调用了Pavzner之前做的一个称为Eulerian Copy Number的算法来计算的.
8.将repeat graph中的非重复边删去,就称为“Tangles”其刻画了sub-repeats的连接关系.
9.步骤6得到的结果,进一步利用mate-pairs的信息来解开部分repeats.(个人理解,具体的内容,这篇文章说详细内容在这篇Pevzner, P. and Tang, H. 2001. Fragment assembly with double-barreled data. Bioinformatics 17: S225–S233.)
10.Simple path输出为contig,再进一步用Euler Scaffolding algorithm组装为scaffold.
Trailer
这篇博客,我们考古了04年的FragmentGluer,主要是向大家介绍repeat graph的思想,尤其是Constructing ${A}$-Bruijn Graph Without the Similarity Matrix这个部分,在充分理解了之后,希望大家移步文献分享:Assembly of long, error-prone reads using repeat graphs Assembly,这篇博客我们将介绍Pavel A. Pevzner的Flye算法.