In this blog, we will check out a theoretical paper about edit distance. In fact edit distance is a kernel idea for sequence alignment in bioinformatics. There are many available tools developed to solve various kinds of alignment scenario. While there exists a gap between theoretical algorithms and practical tools. In practice, we also embed some heuristic part to the tools to facilitate alignment. As theoreticians, they need to figure out some techniques to get a theoretical analysis of these tools that is more close to the practical performance. Further, a good theoretical analysis will light the direction of improvement.

This paper proposed a framework based on the classic NW algorithm with running time $\mathcal{O}(n\lg n)$ and get edit distance with high probability, which is also adapted by many classic implements, like BLAST. Hence, the analysis of the algorithm mentioned in this paper is also a theoretical justification of these heuristic-based alignment tools.

Preliminaries and Definitions

Problem Setup

Given a uniformly random bitstring ${s_1 \sim \{0,1\}^n}$. We generate $s_2$ by $s_1$ via indel channel. For the $j$th bit of $s_1$, $b_j:=(s_1)_j$:

• $b_j$ is substituted i.e. flip, with probability $p_s$.

• $b_j$ is deleted with probability

  • $p_d$ if the previous bit $b_{j-1}$ was not deleted;

  • $q_d$ ($>p_d$) if the previous bit $b_{j-1}$ was deleted;

• An insertion event occurs with probability $p_i$, inserting a uniformly random bit string ${t \sim \{0,1\}^I}$ with length $I \sim \text{Geo}(1-q_i)$ to the right of $b_j$. Inserted bits are not further acted upon by the indel channel. (here the probability of geometric distribution $\Pr(I=k)=(q_i)^{k-1}(1-q_i)$, we can set a unfair coin and the number of times we first get a “head” is $I$).

Each operation is call an edit, and use $\mathcal{E}$ to denote the set of edits generated in the indel channel. Each mutation independently happens for each bit and across different bits. We assume \(\begin{equation} p_s \leq \rho_s, \quad p_d \leq \rho_d,\frac{1-\rho_d}{1-q_d} \leq \rho_d', \quad p_i \leq \rho_i, \frac{1}{1-q_i} \leq \rho_i' \end{equation}\) are hold for some small constants ${\{\rho\}:=\{\rho_s,\rho_d,\rho_d’,\rho_i,\rho_i’\}}$. We denote the distribution of tuples $(s_1,s_2,\mathcal{E})$ as $ID(n)$, i.e. $(s_1,s_2,\mathcal{E}) \sim ID(n)$ generated by some probability $p,q$. Given $(s_1,s_2,\mathcal{E}) \sim ID(n)$, then we can compute edit distance $ED(s_1,s_2)$. Formally, this paper proposes following main theorem.

Theorem 2. Assuming $(1)$ holds for certain constants ${\{\rho\}}$, there exists a (deterministic) algorithm running in time $\mathcal{O}(n \ln n)$ that computes $ED(s_1,s_2)$ for $(s_1,s_2,\mathcal{E}) \sim ID(n)$ with probability $1-n^{-\Omega(1)}$.

Preparation and Lemma

Fact 4 (Chernoff Bound). Let $X_1 \cdots X_n$ be independent Bernoulli random variables and $X=\sum_{i=1}^n X_i, \mu = \mathbb{E}[X]$. Then for $0 < \epsilon <1$:

\[\Pr[X\geq (1+\epsilon)\mu] \leq e^{-\frac{\epsilon^2\mu}{3}},\quad \Pr[X\leq (1-\epsilon)\mu] \leq e^{-\frac{\epsilon^2\mu}{2}},\]

Consider the insertion process, the number of times $m$ for insertion for whole bitstring is a Binomial distribution with probability $p_i$, and the number of insertion bits is a negative binomial distribution with $m$ and probability $q_i$. (This process like that flipping an unfair coin and getting $m$ heads). So, we bound the process in following lemmas.

Fact 5 (Negative binomial tail bound). Let $X\sim NBinom(m,q)$, then

\[\Pr[X \geq k n /p] \leq e^{-\frac{kn(1-1/k)^2}{2}}\]

Proof. If we need more than $kn/p$ times to get $n$ success events, that means when we flip $kn/p$ times, the total number $Y$ of success events is less than $n$, i.e.

\[\Pr[X \geq k n /p] = \Pr[Binom(kn/p,p)<n]\]

Then, we can apply Chernoff bound, get the bound

\[\Pr[Y < n] = \Pr[Y < (1 - (1- 1/k)) kn] \leq e^{-\frac{kn(1-1/k)^2}{2}}\]

Proof done. $\square$

Lemma 6. Consider $X\sim NBinom(m,q)$, where $m=\sum_{i=1}^t m_i, m_i \sim Bern(p_i)$. Then for $1< \alpha \leq 4, \mu=\sum_{i=1}^t p_i$:

\[\Pr \left[X \geq \alpha \cdot \frac{\mu}{q}\right] \leq e^{-\frac{(\sqrt{\alpha}-1)^2\mu}{3}} + e^{-\alpha\mu \frac{(1-1/\sqrt{\alpha})^2}{2}}\]

Definitions

Definition 7. Consider the dependency graph of the edit distance dynamic programming table. The edit distance between $s_1,s_2$ denoted as $ED(s_1,s_2)$ is the weighted shortest path from $(0,0)$ to $(n_1,n_2)$.

Fact 8. (Needleman–Wunsch algorithm): Edit distance between $s_1,s_2$ of length $n_1,n_2$ can be computed in $\mathcal{O}(\vert V \vert + \vert E\vert )$ time by dynamic programming. If we know the dependency graph is contained in vertex set $V’$, we can compute edit distance in $\mathcal{O}(\vert V’ \vert)$ time by deleting $V \setminus V’$ in dependency graph.

Definition 9. An alignment of two string $s_1,s_2$ is any path ${A=\{(i_1=0,j_1=0),(i_2,j_2),\cdots,(i_L=n_1,j_L=n_2)\}}$ from from $(0,0)$ to $(n_1,n_2)$. The set of all alignments is denoted as $\mathcal{A}$.

Definition 10. For $(s_1,s_2,\mathcal{E}) \sim ID(n)$, the canonical alignment of $s_1,s_2$, denoted $A^*$, is the alignment corresponding to $\mathcal{E}$. (We chose each edge/path in dependency graph based on each edit in $\mathcal{E}$).

We should notice that the optimal alignment could not be canonical alignment. For alignments which aren’t the canonical alignment, we characterize their differences from the canonical alignment in the following way.

Definition 11. Fix a canonical alignment $A^*$, and let $A$ be any alignment. A break of $A$ (from $A^*$) is any subpath ${\{(i_1,j_1),(i_2,j_2)\cdots(i_L,j_L)\}}$ of $A$ such that $(i_1,j_1),(i_L,j_L)$ are in $A^*$ but none of $(i_2,j_2)$ to $(i_{L-1},j_{L-1})$ are in $A^*$. The length of break is the value $i_L-i_1$.

​ For $(s_1,s_2,\mathcal{E}) \sim ID(n)$, a break is long if its length is at least $k \ln n$ and short otherwise. An alignment is good if it has no long breaks and bad if it has at least one long break.

Definition 12. (Short and Long Break Replacement). We define $\mathcal{SBR}:\mathcal{A}\mapsto \mathcal{A}$ as a function such that for any alignment $A$, $\mathcal{SBR}(A)$ is the alignment arrived at by applying the following modification to all short breaks in $A$: For a short break from $(i_1,j_1)$ to $(i_L,j_L)$, replace it with the subpath of $A^*$ from $(i_1,j_1)$ to $(i_L,j_L)$. We define $\mathcal{LBR}$ analogously.

Substitution-Only Case

First, let’s consider the simplest case, we only consider substitution here and canonical alignment $A^*$ is just the diagonal ${\{(0,0),(1,1) \cdots (n,n)\}}$. We will show following theorem

Theorem 13. For $(s_1,s_2,\mathcal{E}) \sim ID(n)$ with $p_i,p_d=0$, suppose $p_s \leq \rho_s$, where $\rho_s = 0.028$, there is an $\mathcal{O}(n\ln n)$ time algorithm for computing $ED(s_1,s_2)$ which is correct with probability $1- n^{-\Omega(1)}$.

Proof sketch:

1. Algorithm: Call canonical DP on the dependency graph, which is deleted each entry $(i,j)$ s.t. $\vert i-j\vert > k \ln n$.

2. “Off-diagonal” alignment $A$ (sharing no edge with $A^$) is greater than $A^$ with high probability (shown in Lemma 14).

3. Lemma 17 (proved through Lemma 14) tells us with high probability, all the alignments in the range of $\mathcal{SBR}$ satisfy $A \geq A^*$. Then, if this condition holds, the lowest-cost good alignment is also the best alignment in whole DP (Corollary 16). $\mathcal{LBR}(A)$ is a good alignment and satisfies

\[\forall A, \mathcal{LBR}(A) - A = \mathcal{LBR}(\mathcal{SBR}(A)) - \mathcal{SBR}(A) = A^* - \mathcal{SBR}(A) \leq 0\]

So, even we only consider the best alignment on trimmed dependency graph, we can still get best alignment on global one. $\square$

Lemma 14. For $(s_1, s_2, \mathcal{E}) \sim ID(n)$, with probability $1 - e^{-\Omega(n)}$, $A > A^*$ for all alignments $A$ such that $A$ and $A^*$ do not share any edges.

Proof. The cost of $A^*$ can be upper bounded using a Chernoff bound: The expected number of substitutions is at most $\rho_s n$, so Fact 4 gives

\[\Pr\left[ A^* \leq \frac{3}{2} \rho_s n \right] \leq 1 - e^{-\frac{\rho_s n}{12}}.\]

Now our goal is following:

1. If $A$ shares no edge with $A^*$, $A> cn$, (where $c = \frac{3}{2} \rho_s$) with high probability.
2. $\Rightarrow$: If $A$ shares no edge with $A^*$, $A < cn$, with very low probability.

We achieve this using a union bound over alignments, grouping alignments by their number of deletions $d$ (notice that in substitution-only case, $d$ is also the number of insertions, because we need go back to the right-bottom element). We can ignore alignments with more than $cn/2$ deletions, as they will of course have cost more than $cn$ (we also have $cn/2$ insertions).

\[\begin{equation} \begin{aligned} \Pr[\exists A, A \leq cn] &\leq \sum_{d=1}^{cn/2} \sum_{A \text{ with } d \text{ deletions}} \Pr[A \leq cn] \\ &\leq \sum_{d=1}^{cn/2} \binom{n+d}{d, d, n-d} \Pr\left[ \text{Binom}(n-d, \frac{1}{2}) \leq cn - 2d \right] \\ &\leq \frac{cn}{2} \binom{(1 + \frac{c}{2})n}{\frac{c}{2}n, \frac{c}{2}n, (1 - \frac{c}{2})n} \Pr\left[ \text{Binom}((1 - \frac{c}{2})n, \frac{1}{2}) \leq cn \right]. \end{aligned} \end{equation}\]

Second line: Given $d$ deletions, we know the total number of edge covered by alignment is $n+d$, we need assign $d$ deletions, $d$ insertions a and $n-d$ diagonal edges (substitutions/matches). Obviously, $d$ deletions and $d$ insertions will cause $2d$ in $A$. Then, we can only have at most $cn-2d$ substitutions. Because, we don’t have any information about these edges, so the weight of each edge can be treat as a Bernoulli process with probability as $1/2$, which is distributed uniformly at random. So the total cost of these edges is given by $\text{Binom}((1 - \frac{c}{2})n, \frac{1}{2})$.

Third line: An upper bound for simplicity. Each item are bound by following two formulea

\[\begin{equation} \begin{aligned} \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})n, \frac{1}{2}\right) \leq cn \right] &= \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})n, \frac{1}{2}\right) \leq \left(1 - \frac{2 - 5c}{2 - c} \right) \frac{1}{2}(1 - \frac{c}{2})n \right] \\ &\leq \left[\exp\left( \frac{-(2 - 5c)^2}{8(2 - c)} \right)\right]^n. \end{aligned} \end{equation}\]

Next we upper bound the trinomial using Stirling’s approximation:

\[\begin{equation} \begin{aligned} \binom{(1 + \frac{c}{2})n}{\frac{c}{2}n, \frac{c}{2}n, (1 - \frac{c}{2})n} &\leq \frac{e}{(2\pi)^{3/2}} \frac{((1 + \frac{c}{2})n)^{(1 + \frac{c}{2})n + \frac{1}{2}}}{(\frac{c}{2}n)^{cn + 1}((1 - \frac{c}{2})n)^{(1 - \frac{c}{2})n + \frac{1}{2}}} \\ &\leq \frac{e}{(2\pi)^{3/2}} \frac{1}{n} \left[ \frac{(1+\frac{c}{2})^{(1+\frac{c}{2})n} \cdot (1+\frac{c}{2})^{\frac{1}{2}} } {\frac{c}{2}^{cn} \cdot \frac{c}{2} \cdot (1-\frac{c}{2})^{(1-\frac{c}{2})n} \cdot (1-\frac{c}{2})^{\frac{1}{2}}} \right]\\ &\leq \frac{e}{(2\pi)^{3/2}} \frac{2}{cn} \sqrt{\frac{1 + \frac{c}{2}}{1-\frac{c}{2}}} \left[ \frac{(1+\frac{c}{2})^{(1+\frac{c}{2})n} } {\frac{c}{2}^{cn} \cdot (1-\frac{c}{2})^{(1-\frac{c}{2})n}} \right]\\ &\leq \frac{e}{(2\pi)^{3/2}} \frac{2}{cn} \sqrt{\frac{2 + c}{2-c}} \left[ \frac{(1+\frac{c}{2})^{(1+\frac{c}{2})n} } {\frac{c}{2}^{cn} \cdot (1-\frac{c}{2})^{(1-\frac{c}{2})n}} \right]\\ \end{aligned} \end{equation}\]

For the above bound to be exponentially decaying in $n$, we need that:

\[\frac{(1 + \frac{c}{2})^{(1 + \frac{c}{2})}}{(\frac{c}{2})^c (1 - \frac{c}{2})^{(1 - \frac{c}{2})}} \exp\left( \frac{-(2 - 5c)^2}{8(2 - c)} \right) < 1\]

which holds as long as $c \leq 0.042$, i.e. $\rho_s \leq .028$. For these values of $c$, with high probability $A^* < cn$ and $A > cn$ for any $A$ which does not share any edges with $A^*$. $\square$

Fact 15. Fix any $s_1, s_2, \mathcal{E}$ in the support of $ID(n)$, and let $A, A’$ be any two alignments with the same set of long breaks. Then $\mathcal{LBR}(A) - A = \mathcal{LBR}(A’) - A’$.

Proof. Applying $\mathcal{LBR}$ to $A, A’$, then we just change the long break in each alignment. Because their long break is same, so their difference on these long breaks will be equal. $\square$

Corollary 16. Fix any $(s_1, s_2, \mathcal{E})$ in the support of $ID(n)$. If for all alignments $A$ in the range of $\mathcal{SBR}$, $A \geq A^*$, then any lowest-cost good alignment is also a lowest-cost alignment.

Proof. $\forall$ alignment $A$, $\mathcal{LBR}(A)$ (a good alignment) satisfies $\mathcal{LBR}(A) \leq A$, shown as follow:

\[\mathcal{LBR}(A) - A \stackrel{\text{Fact 15}}{=} \mathcal{LBR}(\mathcal{SBR}(A)) - \mathcal{SBR}(A) = A^* - \mathcal{SBR}(A) \leq 0.\]

So the lowest-cost good alignment is also the lowest cost alignment. $\square$

Lemma 17. For $(s_1, s_2, \mathcal{E}) \sim ID(n)$, with probability $1 - n^{\Omega(1)}$ for all alignments $A$ in the range of $\mathcal{SBR}$, $A \geq A^*$.

Proof.

1. Define the set $A_i$ contained in the range of $\mathcal{SBR}$, which contains all alignments $A$ for which the sum of the lengths of breaks of $A$ from $A^*$ is in $[ik \ln n, (i + 1)k \ln n]$. Then the sets ${A_i : 0 \leq i \leq \frac{n}{k \ln n} }$ forms a disjoint cover of the range $\mathcal{SBR}(A)$. Note that elements of $A_i$ have at most $i$ breaks from $A^*$, each of length at least $k \ln n$. Also note that $A_0$ is a singleton set containing only $A^*$.

2. Define breakpoint configuration of $A$: the set of starting and ending indices of all breaks of $A$ (to simplify future analysis, we index with respect to $s_1$).
3. Furthermore, we continue split $A_i$. Let $B_i$ be the set of all possible breakpoint configurations of alignments in $A_i$. Here, $B \in B_i$ is a binary assignment of each edge in $A^*$ to either agree or disagree with $A \in A_i$. For a fixed set of breakpoint $B \in B_i$, let $A_B$ be the set of all alignments having the breakpoints corresponding to $B$ (i.e. every alignment in $A_B$ has the same breaks from $A^*$). Note that the set ${\{A_B : B \in B_i\}}$ forms a disjoint cover of $A_i$.

We want to show with high probability $\forall A$ in the range of $\mathcal{SBR}$, $A \geq A^*$.

• To achieve this, we first are going to show the probability for existing an alignment in $\mathcal{A}_B$ lower than $A^*$ is quite low. We know that $A < A^*$ iff $(A)_B < (A^*)_B$ where $(A)_B$ denote the restriction of an alignment $A$ to indices $B$. Then, we can bound this probability by applying Lemma 14. For $(A)_B$ and $(A^*)_B$, they don’t share any edge. (Note the proof of Lemma 14 doesn’t assume continuity of alignment.)

\[\Pr[\exists A \in \mathcal{A}_B, A < A^\*] = \Pr[\exists A \in \mathcal{A}_B, (A)_B < (A^\*)_B] \leq n^{-\Omega(ik)}\]

• Then, we will given the bound of probability of existing an alignment in $\mathcal{A}_B$ lower than $A^*$

\[\begin{equation} \begin{aligned} \Pr[\exists A \in \mathcal{SBR}(A), A < A^*] &= \sum_{i=1}^{\frac{n}{k \ln n}} \Pr[\exists A \in A_i, A < A^*] \\ &= \sum_{i=1}^{\frac{n}{k \ln n}} \sum_{B \in B_i} \Pr[\exists A \in A_B, A < A^*] \\ &\leq \sum_{i=1}^{\frac{n}{k \ln n}} \sum_{B \in \mathcal{B}_i} n^{-\Omega(ik)} = \sum_{i=1}^{\frac{n}{k \ln n}} |B_i| n^{-\Omega(ik)}. \end{aligned} \end{equation}\]

Now we must bound the size of $B_i$. We claim that each $B \in B_i$ can be uniquely mapped to $i$ or less contiguous subsets of $[n]$, each of a size in $[k \ln n, 2k \ln n)$ or size $0$ (if the break is longer than $2k \ln n$, we map to a series of consecutive subsets). There are $n$ different possible start positions, and $k \ln n$ different possible end position, so

\[\begin{equation} |B_i| \leq (nk \ln n + 1)^i. \end{equation}\]

Then, the final upper bound is, $s = (nk \ln n + 1)n^{-\Omega(k)} < 1$

\[\begin{equation} \begin{aligned} \Pr[\exists A \in \mathcal{SBR}(A), A < A^*] &\leq \sum_{i=1}^{\frac{n}{k \ln n}} (nk \ln n + 1)^in^{-\Omega(ik)} \\ &= \sum_{i=1}^{\frac{n}{k \ln n}} ((nk \ln n + 1)n^{-\Omega(k)})^i \\ & = \frac{s (1-s^{\frac{n}{k \ln n}})}{1 -s} \\ & \leq c n^{-\Omega(k)} = n^\Omega(k) \end{aligned} \end{equation}\]

Proof done! $\square$

Finding an Approximate Alignment

We know consider the case where insertions and deletions are all present.

Definition 18. Given an alignment $A$, $f_A:[n] \rightarrow \mathbb{Z}$ be the function such that for all $i \in [n]$, $(i,f_A(i)$ is the first vertex in $A$ of the form $(i,j)$.

Properties of the Indel Channel

To simplify presentation, let $\kappa_n = \rho_i \rho_i’ + (\rho_d + 1/k \ln n)(\rho_d’ +1)$.

Lemma 19. For $(s_1,s_2,\mathcal{E}) \sim ID(n)$, let $s_1’$ be the substring formed by bits $i$ to $i+k\ln n -1$ of string $s_1$, and $s_2$ be the substring formed by bits $f_{A^*}(i)$ to $f_{A^*}(i+k \ln n)-1$ of $s_2$. Then:

\[\Pr_{(s_1,s-2,\mathcal{E})\sim ID(n)} \left[ED(s_1',s_2') \geq \frac{3}{2} (\rho_s + \kappa_n) k \ln n \right] \leq n^{-\rho_s k /12} + 2n^{-\rho_i k /60} + 3n^{-\rho_d k /60}\]

Proof. We calculate the upper bound of edit distance by take the union bound of three types of mutation.

1. Substitution: the expectation is at most $\rho_s k \ln n$. Each substitution is a Bernoulli experiment, so we can calculate the Chernoff bound, $\Pr[\text{Substitution}\geq \frac{3}{2}\rho_s k \ln n]] \leq e^{-\rho_s k \ln n /12} \leq n ^{-\rho_s k/12}$.

2. Insertion: the number of insertion is $p_i \frac{1}{1-q_i} k \ln n$ in expectation, and at most $\rho_i \rho_i’ k \ln n$. With $\alpha=3/2$, we can apply lemma 6 to get the bound of $NBinom(Binom(k \ln n, \rho_i), 1/ \rho_i’)$ is at most $2n ^{-\rho_ik/60}$.

3. Deletion: we consider a slightly different process here to simplify analysis

   • For each bit of “type 1” deletion, the probability is $p_d$. But for the first bit of substring, we don’t know if there has deletion before, so we set probability $q_d$ for bit $1$.

   • If bit $j$ has a type 1 deletion, then we sample $\delta\sim Geo(\frac{1-q_d}{1-p_d})$. Then $\Delta$ be the number of bits between $j$ and next bit with type $1$ deletion. A type 2 deletion occurs on the ${\min\{\delta,\Delta\}}$ bits after $j$. Why choose this distribution, because if bit $j-1$ takes type 1 deletion, the overall probability of bit $j$ takes deletion is

     \[\Pr[\text{type 1}] + \Pr[\text{type 2} \mid \text{type 1 not taken}] = p_d + (1-p_d) \frac{q_d-p_d}{1-p_d} = q_d\]

     Hence, we set random variable $Y$ and $X$ for type $1$ and type $2$ deletion. Then $Y \sim Binom(k\ln n -1 ,p_d) + Bero(q_d)$, and $X \sim NBinom(Y,\frac{1-q_d}{1-p_d})$. Hence, the probability of $Y$ exceeds $\frac{3}{2}(\rho_d k \ln n)+1$ is at most $n^{-\rho_d k /12}$ by Chernoff bound. The probability of $X$ exceeds $\frac{3}{2}(\rho_d k \ln n +1)\rho_d’$ is bound by lemma 6, that is $2n ^{-\rho_d k/60}$. So, the total bound is $3n^{-\rho_d k /60}$. $\square$

Lemma 20. Let $s_1,s_2$ be bitstrings of length $k\ln n$, chosen independently and uniformly at random from all bitstrings of length $k \ln n$. Then $\Pr[ED(s_1,s_2)\leq D]\leq \frac{(4e \frac{k \ln n}{D} + 5 e + \frac{4e}{D})^D}{2^{k \ln n}}$.

Lemma 21. For constant $k>0, i \leq n - k\ln n$,

\[\Pr_{(s_1,s_2,\mathcal{E})\sim ID(n)} \left[ \vert f_{A^*}(i+k \ln n) - f_{A^*}(i) - k \ln n \vert \leq \frac{3}{2} \kappa_n \cdot k \ln n\right] \geq 1- 2n^{-\rho_i k /60} - 3n^{-\rho_d k /60}\]

Proof. $\vert f_{A^*}(i+k \ln n) - f_{A^*}(i) - k \ln n \vert$ is the difference between the number of insertions and deletions in the range of $[i, i+ k\ln n -1]$ of $s_1$. So the upper bound is the union of the upper bound of insertion and deletion argued in Lemma 19. $\square$

Corollary 22. Consider the following random process, which we denote $\mathcal{P}$: we choose $i_1 < n - k \ln n$, sample $(s_1, s_2, \epsilon) \sim ID(n)$, and then choose an arbitrary $i_2$ such that $\vert i_2 - f_{A^*}(i_1) \vert \leq k \ln n$ and $i_2$ is at least $k \ln n$ less than the length of $s_2$. Let $s_1’$ denote the string consisting of bits $i_1$ to $i_1 + k \ln n - 1$ of $s_1$ and $s_2’$ the string consisting of bits $i_2$ to $i_2 + k \ln n - 1$ of $s_2$. Then for any $i_2$ we choose satisfying the above conditions,

\[\Pr_{\mathcal{P}} \left[ED(s_1', s_2') \leq \left(1 + \frac{3}{2} (\rho_s + 2 \kappa_n)\right)k \ln n \right] \geq 1 - 2n^{-\rho_k/12} - 4n^{-\rho_k/60} - 6n^{-\rho_k/60}.\]

Proof.

Here, we have three bitstings will be covered in this proof.

1. $s_1’$: from $i_1$ to $i+k\ln +1$
2. $s_2^*$: a substring of $s_2$, from $f_{A^*}(i_1)$ to $f_{A^*}(i_1+k\ln n)-1$.
3. $s_2’$: from $i_2$ to $i_2 + k \ln n -1$. The start position will be $f_{A^*}(i_1) - k\ln n$ to $f_{A^*}(i_1) + k\ln n$

Our goal is to given the upper bound of $ED(s_1’,s_2’)$, which will be bound by triangle inequality i.e. $ED(s_1’,s_2^*) + ED(s_2^*,s_2’)$.

1. $ED(s_1’,s_2^*)$ can be bounded with high probability by Lemma 19.
2. $ED(s_2^*,s_2’)$: here the difference between the start position will be bounded by $k \ln n$. And the difference between the length of two strings is bounded by Lemma 21.

Add the two upper bounds and the union probability, proof done. $\square$

Corollary 23. Consider the following random process, which we denote $\mathcal{P}$: we choose $i_1 < n - k \ln n$, sample $(s_1, s_2, \epsilon) \sim ID(n)$, and then choose an arbitrary $i_2$ such that

\[\vert i_2 - f_{A^*}(i_1) \vert > \left(\frac{3}{2} \kappa_n + 1\right) k \ln n,\]

and $i_2$ is at least $k \ln n$ less than the length of $s_2$. Let $s_1’$ denote the string consisting of bits $i_1$ to $i_1 + k \ln n - 1$ of $s_1$ and $s_2’$ the string consisting of bits $i_2$ to $i_2 + k \ln n - 1$ of $s_2$. Then for $0 < r < 1$,

\[\Pr_{\mathcal{P}}\left[ED(s_1', s_2') > kr \ln n\right] \geq 1 - \left[\frac{(\frac{4e}{r}+5e+\frac{4e}{k r \ln n})^r}{2}\right]^{k \ln n} - 2n^{-\rho_k/60} - 3n^{-\rho_k/60}.\]

Proof. Basically, this proof tell us if start position $i_2$ goes too far from $f_{A^*}(i_1)$, $ED(s_1’,s_2’)$ will be controlled by Lemma 20. First, by Lemma 21, we know the end position of $s_2^*$ will be not far away. So, with high probability $s_2$ goes beyond the range of $s_2^*$.

In detail, if $i_2 > f_{\ast}(i_1) + \left(\frac{3}{2} \kappa_n + 1\right) k \ln n$, then by Lemma 21 we have with probability $1 - 2n^{-\rho_k/60} - 3n^{-\rho_k/60}$, \(i_2 - f_{\ast}(i_1 + k \ln n) = [i_2 - f_{\ast}(i_1) - k \ln n] + [f_{\ast}(i_1 + k \ln n) - f_{\ast}(i_1 + k \ln n)] \geq \frac{3}{2} \kappa_n \cdot k \ln n - \frac{3}{2} \kappa_n \cdot k \ln n = 0.\)

Then $s_1’$ and $s_2’$ become two random string. Then we can call Lemma 20 with $D=r k \ln n$. $\square$

Algorithm for Approximate Alignment

The algorithm is shown in above figure. Basically, we try to decide some anchors of the approximate alignment $f’$. We start from $f’(1)=1$. We split $s_1$ into $\frac{n}{k \ln n}$ fragments with length $k \ln n$. For each fragment $s_1’$, we try to find the corresponding $s_2’$ to decide the position of first index $i k \ln n +1$ of $s_1’$ i.e. $f’(i k \ln n +1)$. It’s clear the running time will be $\mathcal{O}(\frac{n}{\ln n} \cdot \ln n^2) = \mathcal{n \ln n}$.

Now, how to find $s_2’$ and then decide $f’(i k \ln n +1)$ is important. So, we have to search where the $s_2$ located. By Corollary 22, we know if the start position is near $f_{A^*}(i k \ln n +1)$ the edit distance will be small, and otherwise by Corollary 23, the edit distance will be large. So, we know the range $\frac{3}{2} (\rho_s + \kappa_n) k \ln n$ mentioned in Corollary 23 is sufficient. But the thing is we don’t know where the $f_{A^*}(i k \ln n +1)$ is. But by lemma 19, we know $f_{A^*}(i k \ln n +1)$ is around $i k \ln n +1$ with radius $\left(\frac{3}{2} \kappa_n + 1\right) k \ln n$. That’s the reason why $J$ is doubled $\left(\frac{3}{2} \kappa_n + 1\right) k \ln n$ .

Then we can get following Lemma 24 intuitively.

Lemma 24. For $(s_1, s_2, \epsilon) \sim ID(n)$, APPROXALIGN$(s_1, s_2)$ computes in time $O(n \ln n)$ a function $f’$ such that with probability at least $1 - n^{-\Omega(1)}$, for all $i$ where $f’(i)$ is defined, $\vert f’(i) - f_{A^*}(i) \vert \leq \left(\frac{3}{2} \kappa_n + 1\right) k \ln n$.

Proof. We will show by induction.

Base case: $ \vert f’(1)-f_{A^*}(1) \vert = \vert 1 -1 \vert \leq \lceil (\frac{3}{2} \kappa_n + 1) \cdot k \ln n \rceil$.

Induction Hypothesis: $ \vert f’((i-1)k \ln n))-f_{A^*}((i-1)k \ln n) \vert \leq \lceil (\frac{3}{2} \kappa_n + 1) \cdot k \ln n \rceil$

Let’s check $i$. By Lemma 21, with probability $1 - n^{-\Omega(1)}$, $\vert f_{A^*}((i-1)k \ln n +1) - f_{A^*}(i k \ln n +1) - k \ln n \vert \leq \frac{3}{2} \kappa_n \cdot k \ln n$. Then, we have:

\[\begin{equation} \begin{aligned} &\left\vert \left[ f'((i-1)k \ln n + 1) + k \ln n \right] - f_{A^*}(ik \ln n + 1) \right\vert \\ &\leq\left\vert f'((i-1)k \ln n + 1) + k \ln n - \left[ f_{A^*}((i-1)k \ln n + 1) + k \ln n \right] \right\vert + \\ &\left\vert f_{A^*}((i-1)k \ln n + 1) + k \ln n - f_{A^*}(ik \ln n + 1) \right\vert \\ &=\left\vert f'((i-1)k \ln n + 1) - f_{A^*}((i-1)k \ln n + 1) \right\vert + \\ &\left\vert f_{A^*}((i-1)k \ln n + 1) + k \ln n - f_{A^*}(ik \ln n + 1) \right\vert\\ & \leq \lceil \frac{3}{2} \kappa_n + 1 \rceil \cdot k \ln n + \frac{3}{2} \kappa_n \cdot k \ln n \leq J. \end{aligned} \end{equation}\]

So for some $j$ in the range iterated over by the algorithm, $\left\vert f’((i-1)k \ln n + 1) + (j + k) \ln n - f_{A^*}(ik \ln n + 1) \right\vert \leq k \ln n$ could happen. Thus, by Corollary 22, the minimum edit distance $minED$ found by the algorithm in iterating over the $j$ values is at most $(1 + \frac{3}{2}k(\rho_s + 2\kappa_n)) \ln n < k r \ln n$ with probability at least $1 - n^{-\Omega(1)}$.

By Corollary 23, with probability at least $1 - n^{-\Omega(1)}$ the final value of $f’ (ik \ln n + 1)$ cannot differ from $f_{A^*} (ik \ln n + 1)$ by more than $\left\lceil \left( \frac{3}{2} \kappa_n + 1 \right) \cdot k \ln n \right\rceil$, otherwise, by the corollary 23 with high probability $minED$ would be larger than $k r \ln n$.

To sum up, we have following deduction:

• For some $j$, we can meet the condition of Corollary 22 i.e. the start position $s_2$ is not far from $f_{A^*}(i)$.
• $\Rightarrow$: The $minED$ for some $j$, i.e. $ED(s_1’,s_2’)$ is bounded with high probability. Then we have apply Corollary 23.
• $\Rightarrow$: $\vert f’(ik \ln n))-f_{A^*}(ik \ln n) \vert $ is bounded. Otherwise, with high probability, $minED$ will out of bound.

Then we finish the induction. $\square$

The above Lemma 24 restrict the range of standard DP. In detail, we conduct DP on the entries that are within the distance $k_2 \ln n$ from $(i,f’(i))$ for some $i$, here we can set a sufficiently large $k_2$.

Error Analysis

Lemma 25. For any realization of $(s_1, s_2, \epsilon) \sim ID(n)$, let $s_1’$ be the restriction of $s_1$ to any fixed subset of indices $B$ of total size $\ell \geq k \ln n$, $s_2’$ be the substring of $s_2$ that $A^\ast$ aligns with $s_1$, and let $(A^\ast)_B$ denote the restriction of the alignment $A^\ast$ to indices in $s_1’, s_2’$. Then with probability $1 - e^{-\Omega(\ell)}$, for all alignments $A$ of $s_1’, s_2’$ such that $A$ and $(A^\ast)_B$ do not share any edges.

Basically, Lemma 25 told us, if $(A)_B$ share no edge with $(A^*)_B$, then $A \geq A^*$. Similar with Lemma 19, we know $(A^*)_B$ is bounded by $\frac{3}{2} (\rho_s + \kappa_n) \ell$ with high probability. So, we can show if $(A)_B$ share no edge with $(A^*)N$, $(A)_B$ will exceed this bound with high probability, then we know $(A)_B \geq (A^*)_B$. The main work in Lemma 25 is doing some counting under the condition.

Lemma 26. For $(s_1, s_2) \sim \text{ID}(n)$, with probability $1 - n^{-\Omega(1)}$ for all alignments $A$ in the range of $\mathcal{SBR}, A \geq A^*$.

This is a generalized version of Lemma 17. Then we can apply same procedure in Substitution case. By Lemma 24, we know $f’(i)$ is bounded, and call standard DP within a sufficient large range, which can guarantee that with high probability the range of DP cover the range of $\mathcal{LBR}$, i.e. all the good alignment. So, the locality-optimal in this range with high probability is the optimal in global (Lemma 26).

Approaching to Real Cases

In this paper, we assume distribution of $s_1$ is uniformly randomed, but the real sequence could not be in that way. In this section, we try to approach real situition and take a look what kinds of results we could get.

Poly-A sequence

Let’s first consider $s_1$ be $\textbf{AA} \cdots \textbf{A}$ and $s_2$ is generated by substituion only.

Lemma 14(A). For $(s_1, s_2, \mathcal{E}) \sim ID(n), s_1 = \text{polyA(n)}$, with probability $1 - e^{-\Omega(n)}$, $A > A^*$ for all alignments $A$ such that $A$ and $A^*$ do not share any edges.

Proof. The cost of $A^*$ can be upper bounded using a Chernoff bound:

\[\Pr\left[ A^* \leq \frac{3}{2} \rho_s n \right] \leq 1 - e^{-\frac{\rho_s n}{12}}.\]

We will show: if $A$ shares no edge with $A^*$, $A < cn$, with very low probability.

\[\begin{equation} \begin{aligned} \Pr[\exists A, A \leq cn] &\leq \sum_{d=1}^{cn/2} \sum_{A \text{ with } d \text{ deletions}} \Pr[A \leq cn] \\ &\leq \sum_{d=1}^{cn/2} \binom{n+d}{d, d, n-d} \Pr\left[ \text{Binom}(n-d, \rho_s) \leq cn - 2d \right] \\ &\leq \frac{cn}{2} \binom{(1 + \frac{c}{2})n}{\frac{c}{2}n, \frac{c}{2}n, (1 - \frac{c}{2})n} \Pr\left[ \text{Binom}((1 - \frac{c}{2})n, \rho_s) \leq cn \right]. \end{aligned} \end{equation}\]

Second line: each diagnal edge will be matched otherwsie the substituion happens. So, we have a binomial process for $n-d$ dignal edges with probability $\rho_s$.

Third line: An upper bound for simplicity. Each item are bound by following two formulea

\[\begin{equation} \begin{aligned} \Pr\left[ \text{Binom}\left((1 - \frac{1}{2})n, \rho_s \right) \leq cn \right] & = \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})n, \rho_s\right) \leq \frac{c}{\rho_s (1- \frac{c}{2})} \rho_s (1 - \frac{c}{2})n \right] \\ & = \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})n, \rho_s\right) \leq \frac{\frac{3}{2}}{ (1- \frac{c}{2})} \rho_s (1 - \frac{c}{2})n \right] \\ & = \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})n, \rho_s\right) \leq \left(1 + \frac{1 + c}{2 - c} \right) \rho_s (1 - \frac{c}{2})n \right] \\ \end{aligned} \end{equation}\]

$\epsilon > 0$ here, so we cannot bound it by Chernoff formula.

Lemma 25(A).

Proof. … same old.

\[\begin{equation} \begin{aligned} \Pr\left[ \text{Binom}\left((1 - \frac{1}{2})\ell, \rho_s \right) \leq c\ell \right] & = \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})\ell, \rho_s\right) \leq \frac{c}{\rho_s (1- \frac{c}{2})} \rho_s (1 - \frac{c}{2})\ell \right] \\ & = \Pr\left[ \text{Binom}\left((1 - \frac{c}{2})\ell, \rho_s\right) \leq \left(1 + \frac{1 + c}{2 - c} + \frac{\kappa_n}{\rho_s(1-\frac{c}{2})} \right) \rho_s (1 - \frac{c}{2})\ell \right] \\ \end{aligned} \end{equation}\]

$\epsilon > 0$ here, so we cannot bound it by Chernoff formula.

Repeat case

Suppose the length of repeat is $\tau n$. We consider substitution-only first.

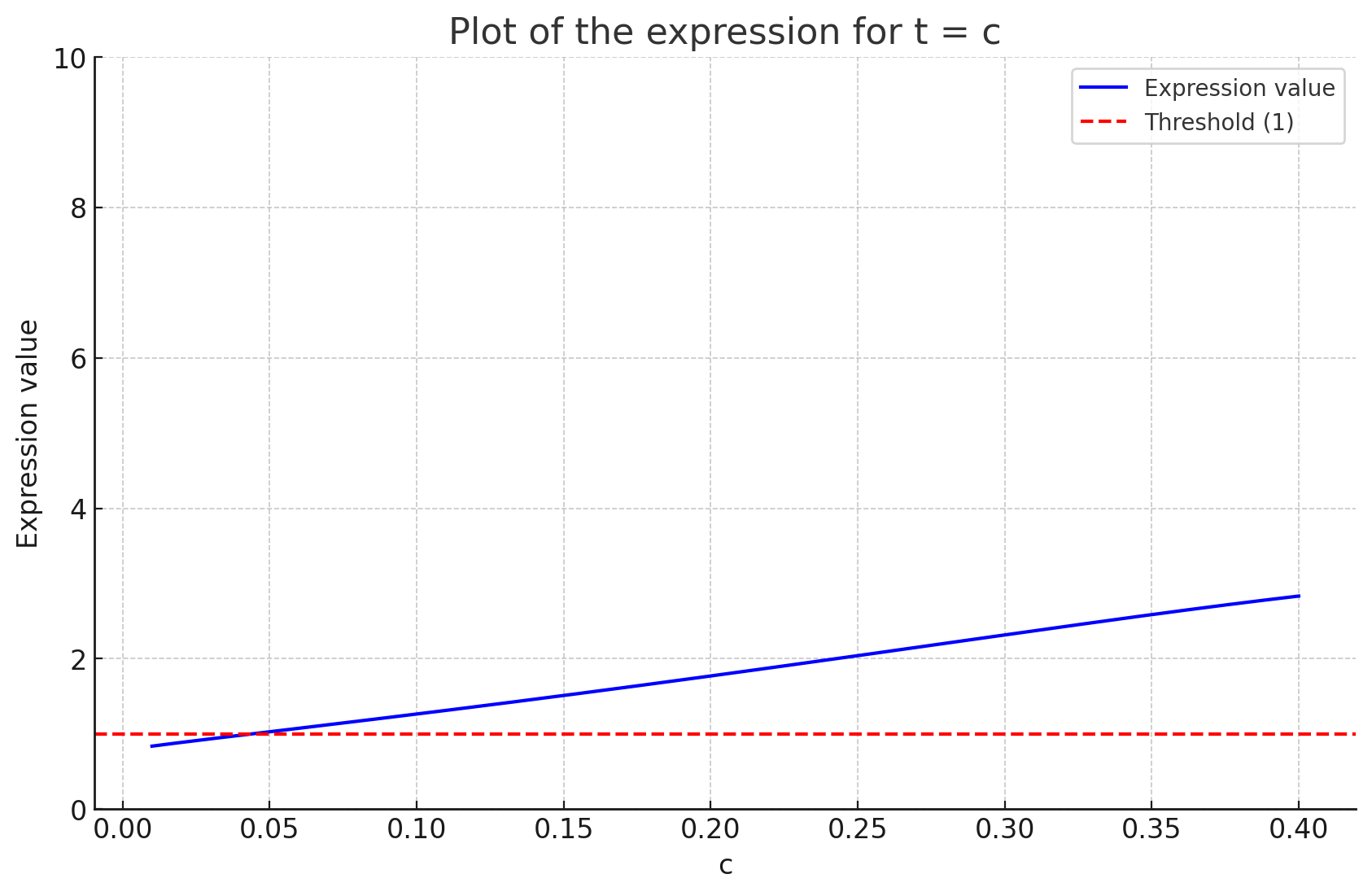
\[\cdots \Pr\left[ \text{Binom}\left((1 - \frac{1}{2} - \tau)n, \rho_s \right) \leq cn \right] \leq\frac{\left(1 + \frac{c}{2}\right)^{\left(1 + \frac{c}{2}\right)}}{\left(\frac{c}{2}\right)^c (1 - \frac{c}{2})^{\left(1 - \frac{c}{2}\right)}} \exp \left( \frac{-(2 - 3c - 2\tau)^2}{8(2 - c - 2\tau)} \right) < 1,\]

$\tau = c$: $c \leq 0.042$

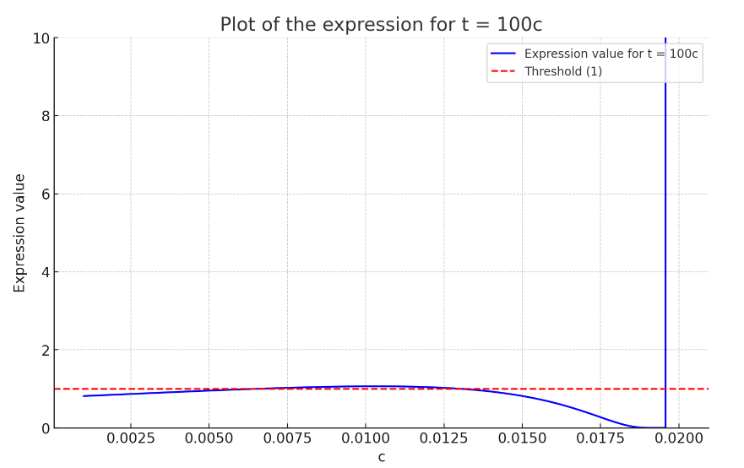
$\tau = 10 c$: $c \leq 0.026$

$\tau = 100$: $c \leq 0.0061$