在这一节我们介绍PVD(Parallel Variable Distribution)算法，也就是所谓的并行变量分配算法

考虑如下的无约束非线性优化问题：

\[\min_{x\in \mathbb{R}^{n}} f(x) \tag{7.1.1}\]

其中$f(x):\mathbb{R}^{n}\rightarrow \mathbb{R}^{1}$为连续可微函数。

PVD算法概要

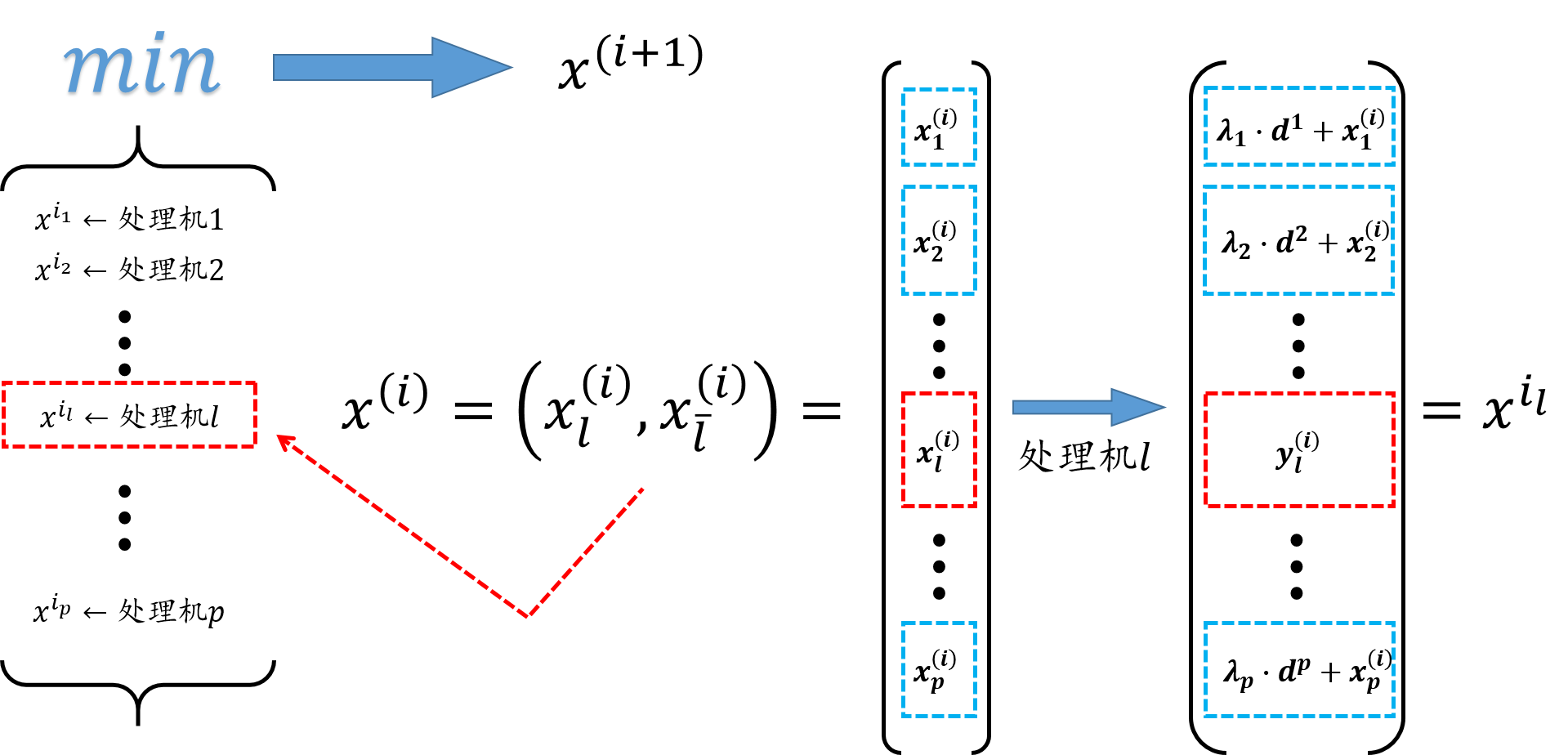
假设可以同时使用 $p$ 个处理机，将问题的变量 $x\in \mathbb{R}^{n}$ 分成 $p$ 块 $x_{1},x_{2},\ldots,x_{p}$ ，第 $l$ 块的变量维数为 $n_{l}$ ，同时 $x$ 的分块满足

\[x=(x^{T}_{1},\ldots,x^{T}_{p})^{T}, x\in \mathbb{R}^{n_{l}}, l=1,2,\ldots,p, \sum_{l=1}^{p} n_{l} = n. \notag\]

将这 $p$ 块变量分配到 $p$ 个处理机上，在每一步根据分块的方式将原问题相地分解为维数较小的 $p$ 个子问题上，每个处理机不仅仅计算自己负责变量的更新，同时沿着给定的方向（每次并行计算之前都要提前给定方向），更新其余处理机对应变量的移动步长，这个称之为”Forget me not”（勿忘我），个人理解：每个处理机不只是更新自己的那部分变量，然后选择 $p$ 个处理机得到的结果中最优的一个作为变量的下一次迭代值 $x^{(i+1)}$.

PVD算法的计算步骤

步骤 $0$ 给定初始点 $x^{0}\in \mathbb{R}^{n}$，任取PVD方向 $\boldsymbol{d}^0\in \mathbb{R}^{n}$ （可以任意选取，如取 $\boldsymbol{d}^{i}=-\nabla f(x^{(i)})/\Vert \nabla f(x^{(i)}) \Vert$ ）.令 $i=0$.若 $\nabla f(x^{(i)}) = \mathbf{0}$.取最优解 $\boldsymbol{x}^{*} = \boldsymbol{x}^{(i)}$ ，算法停止；否则按照如下步骤计算 $\boldsymbol{x}^{(i+1)}$ .

步骤 $1$ （并行计算） 对每个处理机 $l\in \{1,2,\ldots,p\}$ ，计算下面问题的一个近似解 $( \boldsymbol{y}_ {l}^{i},\boldsymbol{\lambda}_ {\bar{l}}^{i} ) \in \mathbb{R}^{n_{l}} \times \mathbb{R}^{p-1}$ :

\[\begin{aligned} \min_{(\boldsymbol{x}_l,\boldsymbol{\lambda}_{\bar{l}})} \psi_{l}^{i} (\boldsymbol{x}_{l},\boldsymbol{\lambda}_{\bar{l}}) &= f(\boldsymbol{x}_{l},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}}), \\ \boldsymbol{x}^{i_{l}} &= (\boldsymbol{y}_{l}^{i},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}}^{i}). \end{aligned} \tag{7.1.2}\]

步骤 $2$ （同步运算） 计算 $x^{(i+1)}$ ，使其满足下面不等式

\[f(\boldsymbol{x}^{(i+1)}) \leq \min_{l\in \{1,2,\ldots,p\}} f(\boldsymbol{x}^{i_{l}}) = \psi_{l}^{i} (\boldsymbol{y}_ {l}^{i},\boldsymbol{\lambda}_ {\bar{l}}^{i}) \tag{7.1.3}\]

令 $i = i + 1$ ，选取新的方向 $d^{i}$; 重复上述步骤.

上述算法中, $\bar{l}$ 表示 $l$ 在集合 $\{1,2,\ldots,p\}$ 中的补集, $D^i_{\bar{l}}$ 为 $(n - n_l)\times(p-1)$ 矩阵,其由相应的PVD方向 $d^i$ (除了第 $l$ 块变量外) 放在矩阵的对角线位置而构成,如下所示

\[\boldsymbol{D}^i_l = \begin{bmatrix} d^i_1 & & & & & & \\ & d^i_2 & & & & &\\ & &\ddots & & & &\\ & & &d^i_{i-1} & & &\\ & & & &d^i_{i+1} & &\\ & & & & &\ddots &\\ & & & & & &d^i_p \end{bmatrix}. \tag{7.1.4}\]

我们通过下面是示意图来理解一下PVD算法做了什么，着重注意步骤 $1$，其实处理器 $l$ 在第 $i$ 次迭代，做了件什么事情呢，就是寻找将 ${x^{(i)}_ l}$ 进行改变，其他处理器对应的方向寻找一个步长系数 ${\lambda}$ 乘上去。所以，针对这 ${p-1}$ 维的 ${\lambda_{\bar{l}}}$ 和 ${n_l}$ 维的 ${x_l}$ 求最小值。

PVD算法的收敛性

下面来讨论一下一下PVD算法的收敛性。首先声明一些记号，对于连续可微的函数 $f:\mathbb{R}^n\rightarrow \mathbb{R}^1$，我们用 $\nabla f$ 来表示 $f$ 的梯度，所谓的梯度是对自变量的 $x$ 的每个分量求偏导，这里用 $\nabla_l f$ 表示 $f$ 关于 $\boldsymbol{x}_l \in \mathbb{R}^{n_l}. l = 1,2,\ldots,p$ 的梯度. 如果 $f$ 在 $\mathbb{R}^n$ 上有连续的一阶偏导数，则记为 ${f\in C^1(\mathbb{R}^n)}$. 如果 ${f}$ 在 ${\mathbb{R}^n}$ 上有常数为 ${K}$ 的 Lipschitz 连续一阶偏导数.即

$$ \Vert \nabla f(y)-\nabla f(x)\Vert \leq K\Vert y-x\Vert,\quad \forall x,y\in \mathbb{R}^n. \notag $$

则记为 ${f\in LC^1_K(\mathbb{R}^n)}$.

引理 7.1.1 如果实数序列 $\{f_i\}$ 不增且有聚点 $\bar{f}$,则 $\{f_i\}$ 收敛到 $\bar{f}$.

证明 首先证明序列 $\{f_i\}$ 下方有界.设 $f_{i_j} \rightarrow \bar{f}$. 若 $\{f_i\}$ 下方无界，则存在 $i,j$ 满足 $$\bar{f} > f_i （因为\{f_i\}是下方无界的），\notag$$ $$f_i \geq f_{i_j} （因为\{f_i\}是非增序列），\notag$$ $$f_{i_j} \geq \bar{f} （因为\{f_{i_j}\}非增加且收敛到\bar{f}）.\notag$$ 矛盾！因此 $\{f_i\}$ 是下方有界的，其又非增，所以一定收敛，且一定收敛到 $\bar{f}$. $\Box$

引理 7.1.2 设 $f\in LC^1_k(\mathbb{R}^n)$,则 $$f(y)-f(x)-\nabla f(x)^T (y-x) \leq |f(y)-f(x)-\nabla f(x)^T (y-x)|\leq \frac{K}{2} {\Vert y-x \Vert}^2.\quad \forall x,y\in \mathbb{R}^n.\notag$$

证明 定理等价于证明下式 $$ f(x+y) -f(x) \leq y^T\nabla f(x)+\frac{K}{2} \Vert y\Vert, \quad \forall x,y\in \mathbb{R}^n. \notag $$ 令 ${g(t)=f(x+ty)}$. 根据链式法则 ${(\frac{dg}{dt})(t)=y^T\nabla f(x+ty)}$，那么可得 $$ \begin{align} f(x+y)-f(x) &= g(1) - g(0) = \int_0^1 \frac{dg}{dt}(t)dt = \int_0^1 y^T\nabla f(x+ty)dt \notag \\ & \leq \int_0^1 y^T\nabla f(x)dt + \left|\int_0^1 y^T\left(\nabla f(x+ty)-\nabla f(x)\right)dt\right| \notag \\ & \leq \int_0^1 y^T\nabla f(x)dt + \int_0^1 \Vert y \Vert \cdot \Vert \nabla f(x+ty)-\nabla f(x)\Vert dt \quad (Cauchy-Schwarz \quad inequation) \notag \\ & \leq y^T\nabla f(x) + \Vert y \Vert \int_0^1 Kt \Vert y \Vert dt \notag\\ & = y^T\nabla f(x)+\frac{K}{2} {\Vert y\Vert}^2.\notag \end{align} \notag $$ 关于绝对值的不等式的证明 $$ \begin{align} f(x+y)-f(x) &= g(1) - g(0) = \int_0^1 \frac{dg}{dt}(t)dt = \int_0^1 y^T\nabla f(x+ty)dt \notag \\ & = \int_0^1 y^T\nabla f(x)dt +\int_0^1 y^T\left(\nabla f(x+ty)-\nabla f(x)\right)dt \notag \\ \end{align} \notag $$ 移项后，取绝对值 $$ \left| f(x+y)-f(x) - \int_0^1 y^T\nabla f(x)dt \right| \leq \left| \int_0^1 y^T\left(\nabla f(x+ty)-\nabla f(x)\right)dt \right| \notag $$ 后续的放缩和上面类似. ${\Box}$

上述定理证明思路来自于文献¹.

PVD的收敛性证明

定理7.1.1（无约束PVD算法的收敛性） 设 ${f\in LC^1_K(\mathbb{R}^n)}$，序列 ${\{\boldsymbol{d}^i\}}$ 有界. 则算法产生的序列 ${\{\boldsymbol{x}^{(i)}\}}$ 或者终止于一个稳定点 ${\boldsymbol{x}^i}$，或者为无限序列，其聚点是 ${f}$ 的稳定点且 ${\lim\limits_{i\rightarrow \infty} \nabla f(\boldsymbol{x}^{(i)}) = \mathbf{0}}$

证明 对 ${l=1,\ldots,p}$，对 ${\psi_l^i}$ 求梯度，有

${\nabla \psi^i_l (\boldsymbol{x}_l,\boldsymbol{\lambda}_{\bar{l}}) = \left[\nabla_l f(\boldsymbol{x}_{l},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}}),\nabla_l f(\boldsymbol{x}_{l},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}})\boldsymbol{D}_{\bar{l}}^{i}\right]. \tag{7.1.5} }$

我们设 ${w=(x_l,\lambda_{\bar{l}})}$，定义 ${n\times(n_l+p-1)}$ 维矩阵 ${\tilde{D}^i_l}$ 为 $$ \tilde{D}^i_l = \begin{bmatrix} d^i_1 & & & & & & &\\ &d^i_2 & & & & & &\\ & &\ddots & & & & &\\ & & &d^i_{i-1} & & & &\\ & & & &\boldsymbol{I}_{n_l} & & &\\ & & & & &d^i_{i+1} & &\\ & & & & & &\ddots &\\ & & & & & & &d^i_p \end{bmatrix}. \notag $$ 其中，${\boldsymbol{I}_{n_l}}$ 表示 ${n_l}$ 阶方阵，并记 ${\tilde{x}^{(i)}_{l} \triangleq (\mathbf{0}_{n_l},x^{(i)}_{\bar{l}})}$，所以 ${ \psi_l^i (\boldsymbol{x}_l,\boldsymbol{\lambda}_{\bar{l}}) = \psi_l^i(w) = f(\tilde{D}^i_l w + \tilde{x}^{(i)}_{l})}$，则 $$\nabla \psi^i_l (\boldsymbol{x}_l,\boldsymbol{\lambda}_{\bar{l}}) = \nabla f(\tilde{D}^i_l w + \tilde{x}^{(i)}_{l})\tilde{D}^i_l = [\nabla_l f(\boldsymbol{x}_{l},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}}),\nabla_l f(\boldsymbol{x}_{l},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}})\boldsymbol{D}_{\bar{l}}^{i}]. \notag$$

因为 ${f}$ 的梯度是 Lipschitz 连续，又 ${\{\boldsymbol{d}^i\}}$ 有界，故 ${\psi_l^i}$ 也是 Lipschitz 连续的.

对于 ${\psi_l^i(w)}$ 的梯度 $$ \begin{align} \left\| \nabla \psi(x) -\nabla\psi(y) \right\| &= \left\| \left[\nabla f(\tilde{D}^i_l x + \tilde{x}^{(i)}_{l}) - \nabla f(\tilde{D}^i_l y + \tilde{x}^{(i)}_{l}) \right] \tilde{D}^i_l \right\| \notag\\ & \leq \left\| \tilde{D}^i_l \right\| \cdot \left\| \nabla f(\tilde{D}^i_l x + \tilde{x}^{(i)}_{l}) - \nabla f(\tilde{D}^i_l y + \tilde{x}^{(i)}_{l}) \right\| \notag\\ & \leq \left\| \tilde{D}^i_l \right\| \cdot K \cdot \left\| \tilde{D}^i_l x + \tilde{x}^{(i)}_{l} - \left(\tilde{D}^i_l y + \tilde{x}^{(i)}_{l} \right) \right\| \notag\\ & \leq {\left\| \tilde{D}^i_l \right\|}^2 \cdot K \cdot \left\|x-y\right\|,\quad \forall x,y\in \mathbb{R}^{n_l+p-1}.\notag \end{align}. \notag $$ 这里面，两次用到 ${\left\|\tilde{D}^i_l w \right\| \leq \left\|\tilde{D}^i_l \right\| \cdot \left\| w \right\|}$，可以认为 ${\tilde{D}^i_l}$ 是一种线性算子，容易验证其为连续（有界）的算子，那么根据泛函有界线性算子的范数定义 ${\left\|A\right\| = sup\{\left\|Ah\right\|:\left\|h\right\|=1}\}$，可以得出 ${\left\|Ah \right\| \leq \left\|A \right\| \cdot \left\| h \right\|}$.

不妨设 ${\psi^i_l}$ 的 Lipschitz 常数为 ${K_1}$. 现在对 ${l=1,\ldots,p}$,定义 ${(\boldsymbol{z}^i_l,\boldsymbol{v}^i_l)} \in \mathbb{R}^{n_l+(p-1)}$ 如下: $$ (\boldsymbol{z}^i_l,\boldsymbol{v}^i_l) = (\boldsymbol{x}_l^{(i)},\mathbf{0}) - \frac{1}{K_1} \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0}).\tag{7.1.6} $$ 根据引理 7.1.2，对 ${l=1,\ldots,p}$,有 $$ \begin{align} \psi^i_l (\boldsymbol{z}^i_l,\boldsymbol{v}^i_l) -\psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})& - \nabla {\psi(\boldsymbol{x}_l^{(i)},\mathbf{0})}^T [(\boldsymbol{z}^i_l,\boldsymbol{v}^i_l)-(\boldsymbol{x}_l^{(i)},\mathbf{0})] \leq \frac{K_1}{2} {\left\|(\boldsymbol{z}^i_l,\boldsymbol{v}^i_l)-(\boldsymbol{x}_l^{(i)},\mathbf{0})\right\|}^2 \notag \\ \psi^i_l (\boldsymbol{z}^i_l,\boldsymbol{v}^i_l) -\psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})& \leq \frac{K_1}{2} {\left\|-\frac{1}{K_1} \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right\|}^2 + \nabla {\psi(\boldsymbol{x}_l^{(i)},\mathbf{0})}^T \left(-\frac{1}{K_1} \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right) \notag \\ \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0}) - \psi^i_l (\boldsymbol{z}^i_l,\boldsymbol{v}^i_l) &\geq -\frac{1}{2K_1} {\left\| \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right\|}^2 + \nabla {\psi(\boldsymbol{x}_l^{(i)},\mathbf{0})}^T \left(\frac{1}{K_1} \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right) \notag \end{align}. \notag $$ 所以，得到 $$ \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0}) - \psi^i_l (\boldsymbol{z}^i_l,\boldsymbol{v}^i_l) \geq \frac{1}{2K_1} {\left\| \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right\|}^2. \tag{7.1.7} $$ 根据算法，每次迭代求得最小的 ${\psi^i_l}$ 值所对应的点 ${( \boldsymbol{y}_ {l}^{i},\boldsymbol{\lambda}_ {\bar{l}}^{i} )}$，所以 $$ \psi_l^i(\boldsymbol{y}_ {l}^{i},\boldsymbol{\lambda}_ {\bar{l}}^{i}) \leq \psi^i_l (\boldsymbol{z}^i_l,\boldsymbol{v}^i_l). \tag{7.1.8} $$ 根据上述两个不等式(7.1.7)和(7.1.8)，对于 ${l=1,\ldots,p}$，有 $$ \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0}) - \psi_l^i(\boldsymbol{y}_ {l}^{i},\boldsymbol{\lambda}_ {\bar{l}}^{i}) \geq \frac{1}{2K_1} {\left\| \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right\|}^2. \tag{7.1.9} $$ 进一步，可得 $$ f(\boldsymbol{x}^{(i)}) - f(\boldsymbol{y}_{l}^{i},\boldsymbol{x}_{\bar{l}}^{(i)} + \boldsymbol{D}_{\bar{l}}^{i}\boldsymbol{\lambda}_{\bar{l}}^{i}) \geq \frac{1}{2K_1} {\left\| \nabla \psi^i_l (\boldsymbol{x}_l^{(i)},\mathbf{0})\right\|}^2 \geq \frac{1}{2K_1} {\left\| \nabla_l f(\boldsymbol{x}^{(i)})\right\|}^2. \tag{7.1.10} $$ 根据 ${\boldsymbol{x}^{i_l}}$ 的定义，我们有 $$ f(\boldsymbol{x}^{(i)}) - f(\boldsymbol{x}^{i_l}) \geq \frac{1}{2K_1} {\left\| \nabla_l f(\boldsymbol{x}^{(i)})\right\|}^2,\quad l=1,\ldots,p. \tag{7.1.11} $$ 因此两边同时对 ${l=1,2,\ldots,p}$ 求和，再除以 ${p}$，可得 $$ f(\boldsymbol{x}^{(i)}) - \frac{1}{p} \sum_{l=1}^p f(\boldsymbol{x}^{i_l}) \geq \frac{1}{2pK_1} \sum_{l=1}^p {\left\| \nabla_l f(\boldsymbol{x}^{(i)})\right\|}^2 =\frac{1}{2pK_1} {\left\| \nabla f(\boldsymbol{x}^{(i)})\right\|}^2. \tag{7.1.12} $$ 根据同步运算的准则，我们选取备选方案中最小的，因此有 $$ f(\boldsymbol{x}^{(i+1)}) \leq \frac{1}{p} \sum_{l=1}^p f(\boldsymbol{x}^{i_l}). \tag{7.1.13} $$ 综合不等式(7.1.12)和(7.1.13)，得到 $$ f(\boldsymbol{x}^{(i)}) - f(\boldsymbol{x}^{(i+1)}) \geq \frac{1}{2pK_1} \left\| \nabla f(\boldsymbol{x}^{(i)}) \right\|^2. \tag{7.1.14} $$ 显然，根据终止条件，当 ${\nabla f(\boldsymbol{x}^{(i)})=\mathbf{0}}$ 时，算法终止于 ${\boldsymbol{x}^{(i)}}$. 如果假设 ${\forall i,\nabla f(\boldsymbol{x}^{(i)}) \neq \mathbf{0}}$ 且有子序列 ${\boldsymbol{x}^{(i_j)}}$ 收敛到 ${\overline{\boldsymbol{x}}}$，则因序列 ${\{f(\boldsymbol{x}^{(i)})\}}$ 是非增序列，且 ${f}$ 是连续函数，则 ${f(\overline{\boldsymbol{x}})}$ 是一个聚点，根据引理 7.1.1， 序列 ${\{f(\boldsymbol{x}^{(i)})\}}$ 收敛到 ${f(\overline{\boldsymbol{x}})}$. 根据式(7.1.14)可知， $$ 0 = \lim\limits_{j\rightarrow \infty} \left(f(\boldsymbol{x}^{(i_j)}) - f(\boldsymbol{x}^{(i_j+1)})\right) \geq \lim\limits_{j\rightarrow \infty} \frac{1}{2pK_1} {\left\| \nabla f(\boldsymbol{x}^{(i_j)})\right\|}^2. \tag{7.1.15} $$ 从而，${\nabla f(\overline{\boldsymbol{x}}) = \mathbf{0}}$. 也就是 ${\{\boldsymbol{x}^{(i)}\}}$ 的聚点是 ${f}$ 的一个稳定点，因为序列 ${\{f(\boldsymbol{x}^{(i)})\}}$ 收敛到 ${f(\overline{\boldsymbol{x}})}$，所以结合(7.1.14)，${\left\| \nabla f(\boldsymbol{x}^{(i)})\right\|^2}$ 被迫收敛，则有 ${\lim\limits_{i\rightarrow \infty} \frac{1}{2pK_1} {\left\| \nabla f(\boldsymbol{x}^{(i)})\right\|}^2}$ 成立. ${\Box}$

PVD线性收敛性

定理7.1.2（无约束PVD算法的线性收敛性）设 ${f\in LC^1_k(\mathbb{R}^n)}$，序列 ${\{\boldsymbol{d}^i\}}$ 有界，且函数 ${f}$ 是强凸，即存在常数 ${\kappa \geq 0}$，使得（强凸函数的定义，比严格凸更强的定义） $$ f(\boldsymbol{y}) - f(\boldsymbol{x}) - \nabla f(\boldsymbol{x})(\boldsymbol{y} - \boldsymbol{x}) \geq \frac{\kappa}{2} \left\| \boldsymbol{y} - \boldsymbol{x} \right\| ^2, \quad \forall \boldsymbol{y},\boldsymbol{x} \in \mathbb{R}^n, \tag{7.1.16} $$ 或者等价地， $$ \left(\nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x})\right)(\boldsymbol{y} - \boldsymbol{x}) \geq \kappa \left\| \boldsymbol{y} - \boldsymbol{x} \right\|^2, \quad \forall \boldsymbol{y},\boldsymbol{x} \in \mathbb{R}^n, \tag{7.1.17} $$ 则PVD算法产生的点列 ${\{\boldsymbol{x}^{(i)}\}}$ 线性收敛到问题(7.1.1)的唯一解 ${\overline{\boldsymbol{x}}}$，且存在常数 ${K>0}$，使收敛速率为 $$ \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\| \leq \left(\frac{2}{\kappa} \left(f(\boldsymbol{x}^{(0)})-f(\overline{\boldsymbol{x}})\right) \right)^{\frac{1}{2}} \left(1-\frac{1}{p} \left(\frac{\kappa}{K}\right)^2 \right)^{\frac{i}{2}}.\notag $$

证明 根据 ${f}$ 的强凸性质，因此 ${\{\boldsymbol{x}^{(i)}\}}$ 至少存在一个极限点 ${\overline{\boldsymbol{x}}}$，根据定理7.1.1，${\{\boldsymbol{x}^{(i)}\}}$ 的任意一个聚点 ${\overline{\boldsymbol{x}}}$ 是问题(7.1.1)的稳定点，根据 ${f}$ 的凸性，其也是问题(7.1.1)的极小点. 再根据 ${f}$ 的严格凸性，其有唯一的极小值点，所以PVD算法产生的点列收敛到唯一解 ${\overline{\boldsymbol{x}}}$. 下面讨论其线性收敛速率. 根据 ${f}$ 的强凸性质，以及 Cauchy-Schwarz 不等式，有 $$ \begin{align} \kappa \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\|^2 & \leq \left(\nabla f(\boldsymbol{x}^{(i)}) - \nabla f(\overline{\boldsymbol{x}}) \right) (\boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}}) \notag \\ & \leq \left\| \nabla f(\boldsymbol{x}^{(i)}) - \nabla f(\overline{\boldsymbol{x}}) \right\| \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\| \notag \\ & = \left\| \nabla f(\boldsymbol{x}^{(i)})\right\| \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\| \notag \\ \end{align}. \notag $$ 根据定理7.1.1的式(7.1.14) （令 ${\alpha = \frac{1}{2pK}}$，因为序列 ${\{\boldsymbol{d}^i\}}$ 有界，所以所有的 ${\psi^i_l}$ 可以有一个共同的满足 Lipschitz 连续的常数，因此 ${\alpha}$ 与 ${i}$ 无关.），有 $$ f(\boldsymbol{x}^{(i)}) - f(\boldsymbol{x}^{(i+1)}) \geq \alpha \left\| \nabla f(\boldsymbol{x}^{(i)}) \right\|^2 \geq \alpha \kappa^2 \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\|^2 \notag $$ 再根据引理7.1.2，可知（请注意 ${x}$ 的上标） $$ \begin{align} f(\boldsymbol{x}^{(i)}) - f(\boldsymbol{x}^{(i+1)}) &\geq \alpha \kappa^2 \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\|^2 \notag \\ & \geq \frac{2 \alpha \kappa^2}{K} \left(f(\boldsymbol{x}^{(i)})-f(\overline{\boldsymbol{x}})-\nabla f(\overline{\boldsymbol{x}})^T (\boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}})\right) \notag \\ & \geq \frac{2 \alpha \kappa^2}{K} \left(f(\boldsymbol{x}^{(i)})-f(\overline{\boldsymbol{x}}) \right) \notag \end{align} \notag $$ 上式等价于， $$ \left(1- \frac{2 \alpha \kappa^2}{K} \right)\left(f(\boldsymbol{x}^{(i)})-f(\overline{\boldsymbol{x}}) \right) \geq f(\boldsymbol{x}^{(i+1)})-f(\overline{\boldsymbol{x}}) \notag $$ 根据递推关系，我们得到， $$ f(\boldsymbol{x}^{(i)})-f(\overline{\boldsymbol{x}}) \leq \left(1- \frac{2 \alpha \kappa^2}{K} \right)^i \left(f(\boldsymbol{x}^{(0)})-f(\overline{\boldsymbol{x}}) \right) \tag{*} $$ 再根据 ${f}$ 的强凸性， $$ f(\boldsymbol{x}^{(i)})-f(\overline{\boldsymbol{x}}) \geq \frac{\kappa}{2} \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\|^2 + \nabla f(\overline{\boldsymbol{x}})^T (\boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}}) \notag $$ 等价于， $$ \left(\frac{2}{\kappa} \left( f(\boldsymbol{x}^{(i)})-f(\overline{\boldsymbol{x}}) \right) \right)^{\frac{1}{2}} \geq \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\| \notag $$ 上式带入(*)式，（替换回 ${\alpha}$） $$ \left\| \boldsymbol{x}^{(i)} - \overline{\boldsymbol{x}} \right\| \leq \left(\frac{2}{\kappa} \left(f(\boldsymbol{x}^{(0)})-f(\overline{\boldsymbol{x}})\right) \right)^{\frac{1}{2}} \left(1-\frac{1}{p} \left(\frac{\kappa}{K}\right)^2 \right)^{\frac{i}{2}}.\notag $$ 至此，我们得到了定理的结论 ${\Box}$

可以发现，PVD算法的收敛速率，受制于一个线性收敛的数列。但是，处理机数量 ${p}$ 增大，收敛速率下降（常数${\left(1-\frac{1}{p} \left(\frac{\kappa}{K}\right)^2\right)}$ 更趋近于 ${1}$）. 这个结果其实有点反直觉的，同时非常让人失望，因为我们用了更多的处理器，但是收敛速度反而慢了. 有一些算法改进了PVD的方向，最终达到了线性收敛比与处理机个数无关的的效果.

Summary

1.PVD算法在并行阶段，将处理机 ${l}$ 对应的变量是完全自由的，同时其他变量对应的方向计算相应的步长，求得最小值点作为一个备选点。

2.同步计算时，选取备选点中最小的作为下一步迭代点，然后给出下一步的方向。

3.线性收敛算法，但是线性收敛比与处理机个数 ${p}$ 负相关或者无关。

Reference